实验目的
熟悉掌握微分方程的求解;会运用Matlab软件求微分方程的数值解;会运用Matlab软件做简单的编程。
实验要求
实验步骤要有模型建立,模型求解、结果分析。
实验内容
(一)微分方程精确解
- 求解微分方程y'=x+x3 ,并作出其积分曲线.
- 求解微分方程y'-(2y/x+1)=(x+1)(5/2),并作出其积分曲线。
(二) 微分方程的数值解
在区间[1,4]上求出微分方程xy'-x2ysinx+1=0,y|x=1=1,的数值解,并作出数值解的图形。
实验步骤
(一)已知题目要求为解出微分方程的精确解,本报告使用MATLAB的dsolve()函数求其解析解,dsolve(‘方程1’,‘方程2’,…,‘方程n’,…,’初始条件’,’自变量’)。
解:(1)本文使用MATLAB求解,在做其积分曲线时,取x从0到1的区间,常数项从-10到10,代码

1 %题1 2 y=dsolve('Dy=x+x^3','x'); 3 figure(1);hold on 4 for C11=-10:1:10 5 x=(0:.1:1); 6 plot(x,C11+(x.^2.*(x.^2 + 2))./4,'LineWidth',2) 7 end
步骤:
1、求出微分方程的通解
>> y=dsolve('Dy=x+x^3','x')
y =
C11 + (x^2*(x^2 + 2))/4
2、作图,运行上述代码
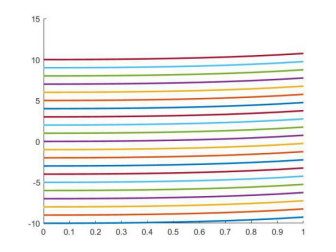
因此解得y=x2(x2+2)/4+c11,积分曲线如上示。当然使用Mathematica求解如下

1 DSolve[y'[x] == x + x^3, y[x], x] 2 t = Table[c + (1/2)*x^2 + (1/4)*x^4, {c, -3, 3}]; 3 Plot[Evaluate[t], {x, -1.5, 1.5}]
运行示例
{{y[x] -> x^2/2 + x^4/4 + C[1]}}
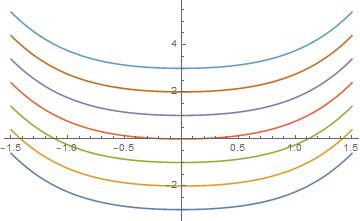
(2)步骤同上,代码

1 y=dsolve('Dy-(2*y)/(x+1)=(x+1)^(5/2)','x'); 2 figure(1);hold on 3 for C13=-10:1:10 4 x=(0:.1:1); 5 plot(x,(2.*(x + 1).^(7/2))/3 + C13.*(x + 1).^2,'LineWidth',2); 6 end
运行示例
>> y=dsolve('Dy-(2*y)/(x+1)=(x+1)^(5/2)','x')
y =
(2*(x + 1)^(7/2))/3 + C13*(x + 1)^2
曲线积分
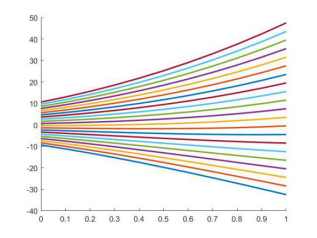
解得, ,图上示。
,图上示。

1 DSolve[y'[x] - 2*y[x]/(x + 1) == (x + 1)^(5/2), y[x], x] 2 t = Table[(x + 1)^2*(2 (x + 1)^(3/2)/3 + c), {c, -3, 3, 2}]; 3 Plot[Evaluate[t], {x, -1, 2}]
运行示例
{{y[x] -> 2/3 (1 + x)^(7/2) + (1 + x)^2 C[1]}}
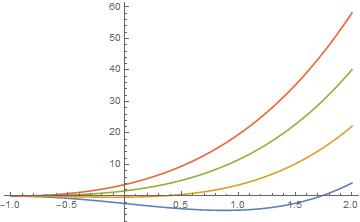
(二)微分方程的数值解
解:数值解,本报告使用MATLAB的ode45函数,步骤如下
先编写函数odefun.m如下

1 function dy=odefun(x,y) 2 %dy=0; 3 dy=x*y*sin(x)-1/x; 4 end
再编写如下代码

1 %题二 2 [T,Y]=ode45('odefun',1:.01:4,1); 3 plot(T,Y(:,1),'-o')
运行示例
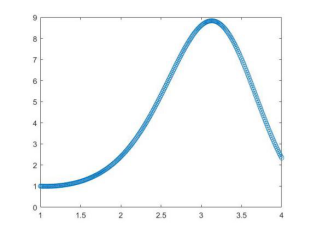
使用Mathematica求解如下

1 Clear[f, x] 2 sol = NDSolve[{x*y'[x] - x^2*y[x]*Sin[x] + 1 == 0, y[1] == 1}, 3 y[x], {x, 1, 4}] 4 f[x_] := Evaluate[y[x] /. sol] 5 Plot[f[x], {x, 1, 4}, PlotRange -> All]

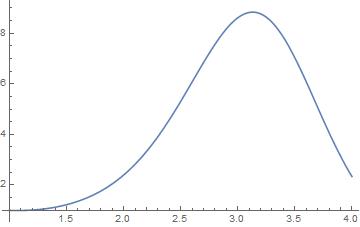
小结
在使用MATLAB求解常微分问题之前,最好先学会手算,否则可能会出现学会了使用MATLAB求解常微分的问题,却不知到得到的答案是什么意思。
