Matlab数值微分

实验目的：

用Matlab实现LU分解和列主元消去法求解线性方程组

实验要求：

1. 给出LU分解算法和列主元消去法算法

2. 用Matlab实现LU分解

3. 用Matlab实现列主元消去法

实验内容：

　　用LU分解及列主元消去法解线性方程组

　　

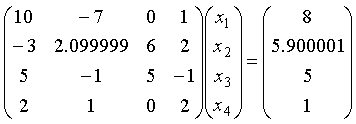
　　输出 Ax=b 中系数 A=LU分解的矩阵L及U，解向量x及detA；列主元法的行交换次序，解向量x及detA；比较两种方法所得的结果。

实验步骤：

　　

 　　代码：

%LU分解算法
%输入：矩阵A和向量b
%输出：det和自变量的值
function [det,x,y,l,u]=LU(A,b)
[m,n]=size(A);
%输入的A与b的行数与列数的限制
if m~=n
    disp('输入错误，系数矩证阵只能是方阵');
end
if n~=length (b)
    disp('输入错误，常数项的个数应与方程的个数相同');
end
for k=1:n-1%主行循环
    for i=k+1:n
        A(i,k)=A(i,k)/A(k,k);
        for j=k+1:n
            A(i,j)=A(i,j)-A(i,k)*A(k,j);
        end
    end
end
l=eye(n);
u=zeros(n,n);
for i=1:n
    for j=1:n
        if j<i
            l(i,j)=A(i,j);
        else
            u(i,j)=A(i,j);
        end
    end
end

y(1)=b(1);
for k=2:n
    s=0;
    for j=1:k-1
        s=s+l(k,j)*y(j);
    end
    y(k)=b(k)-s;
end
x(n)=y(n)/u(n,n);
for k=n-1:-1:1
    s=0;
    for j=k+1:n
        s=s+u(k,j)*x(j);
    end
    x(k)=(y(k)-s)/u(k,k);
end
det=1;
for i=1:n
    det=det*u(i,i);
end
end

　　求解示例：

　　

　　 

 　　

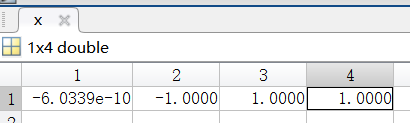
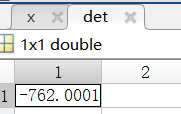
　　2.列主元消去法算法（该算法来源于：C.Jiang老师）：

　　

 　　代码：

%列主元消去算法，求自变量和系数行列式的值
%输入：系数矩阵和因变量，也就是Ax=b,中的A和b
%输出：自变量x和系数行列式det
function [z,det]=liezhu(A,b)
%行列式det初始值为1
det=1;
[m,n]=size(A);
%输入的A与b的行数与列数的限制
if m~=n
    disp('输入错误，系数矩证阵只能是方阵');
end
if n~=length (b)
    disp('输入错误，常数项的个数应与方程的个数相同');
end
%对于k=1,2,...,n-1，对A扫描
for k=1:n-1
    %按列选主元
    p=A(k,k);%记忆当前值
    I=k;
    for i=k:n
        if abs(A(i,k)) > abs(p)%按行扫描该列的最大值
        end
    end
    if I~=k%换行使当前主元绝对值最大
        for j=k:n
            w=A(k,j);%记忆当前主元所在行
            A(k,j)=A(I,j);%换行
            A(I,j)=w;%换行
        end
        %并且把b同时换行
            u=b(k);
            b(k)=b(I);
            b(I)=u;
    end
    %如果得到的最大绝对值是0，则结束程序
    if A(i,k)==0
        det=0;
    end
    %消元计算
    for i= k+1:n
    %对于i=k+1,...,n
        A(i,k)=A(i,k)/A(k,k);
        b(i)=b(i)-A(i,k)*b(k);
        for j=k+1:n
        %对于j=k+1,...,n
            A(i,j)=A(i,j)-A(i,k)*A(k,j);
        end
    end
    %算行列式
    det=A(k,k)*det;
end
%如果最后一个主元等于0，则停止计算。并使行列式等于0
if A(n,n)==0
    det=0;
end
%回代求解
b(n)=b(n)/A(n,n);
%对于i=n-1,...,2,1
for i=(n-1):-1:1
    w=0;
    %得到一个累加值
    for j=(i+1):n
        w=w+A(i,j)*b(j);
    end
    %求得bi
    b(i)=(b(i)-w)/A(i,i);
end
%行列式的值
det=det*A(n,n);
z=b; 
end

　　运行：

　　

 　　

 　　

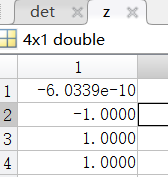
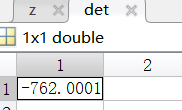
小结：

　　就本例子而言，二者在求得的x和det没有差别。在编写数学类的程序时，务必熟识所用到的数学知识。（文中代码均为zlc所写）