1 概述
在介绍Transformer模型之前,先来回顾Encoder-Decoder中的Attention。其实质上就是Encoder中隐层输出的加权和,公式如下:

将Attention机制从Encoder-Decoder框架中抽出,进一步抽象化,其本质上如下图 (图片来源:张俊林博客):
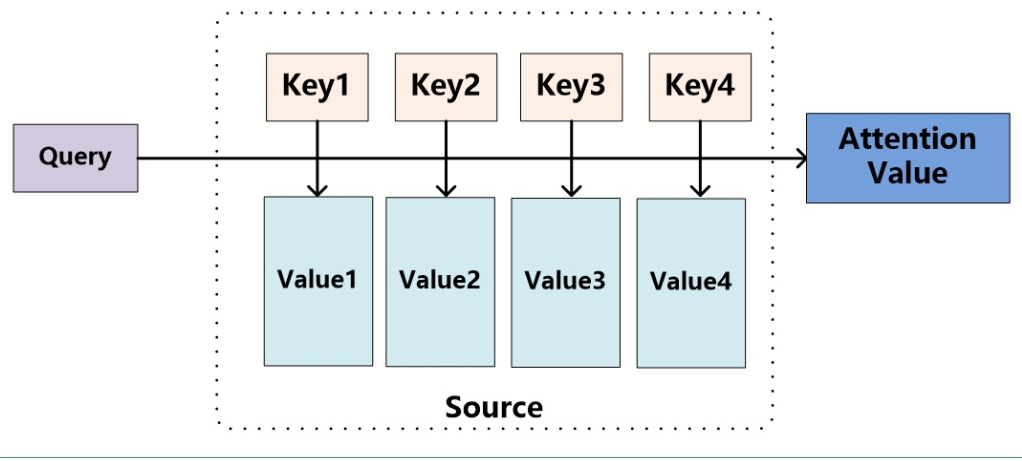
以机器翻译为例,我们可以将图中的Key,Value看作是source中的数据,这里的Key和Value是对应的。将图中的Query看作是target中的数据。计算Attention的整个流程大致如下:
1)计算Query和source中各个Key的相似性,得到每个Key对应的Value的权重系数。在这里我认为Key的值是source的的隐层输出,Key是等于Value的,Query是target的word embedding(这种想法保留)。
2)利用计算出来的权重系数对各个Value的值加权求和,就得到了我们的Attention的结果。
具体的公式如下:
$ Attention(Query, source) = sum_{i=1}^{L_x} Similarity(Query, Key_i) * Value_i $
其中 $L_x$ 代表source中句子的长度。
再详细化将Attention的计算分为三个阶段,如下图(图片来源:张俊林博客)
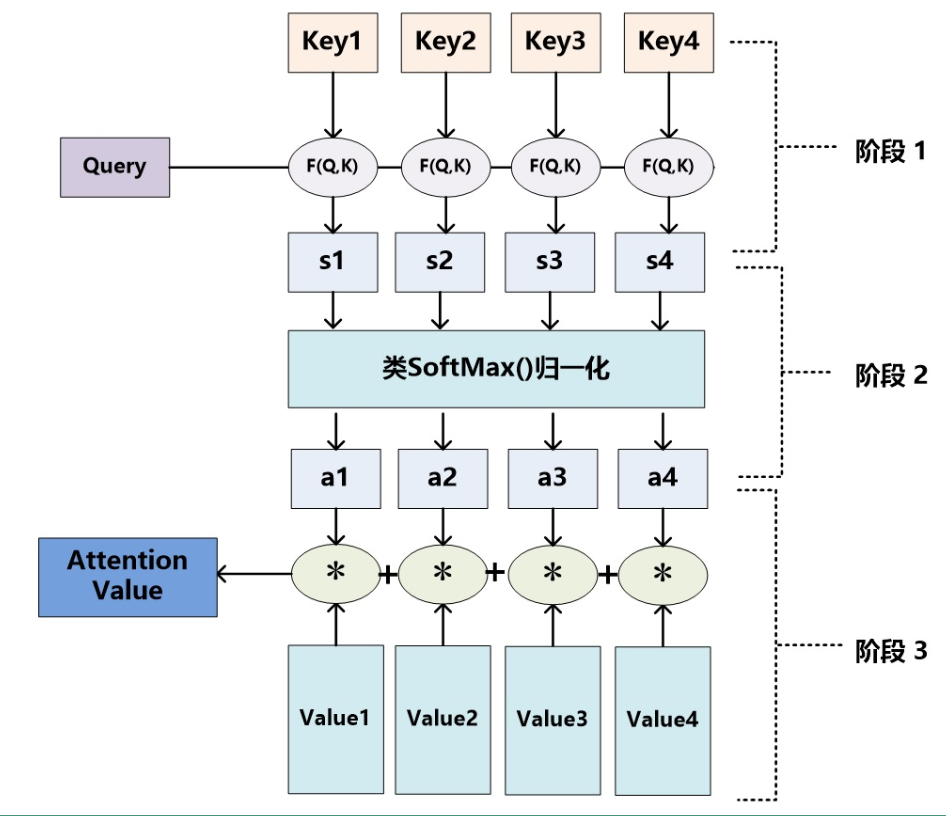
1)计算相似性,在这里计算相似性的方法有多种:点积,Cosine相似性,MLP网络等。较常用的是点积和MLP网络。
2)将计算出的相似性用softmax归一化处理。
3)计算Value值的加权和。
在这里的Attention本质上是一种对齐的方法,也可以将Attention看作是一种软寻址的方法,以权重值将target中的词和source中的词对齐。相对应软寻址(soft-Attention),还有一种hard-Attention,顾名思义就是直接用权值最大的Value值作为Attention。
2 Transformer模型
Transformer模型来源于谷歌2017年的一篇文章(Attention is all you need)。在现有的Encoder-Decoder框架中,都是基于CNN或者RNN来实现的。而Transformer模型汇中抛弃了CNN和RNN,只使用了Attention来实现。因此Transformer是一个完全基于注意力机制的Encoder-Decoder模型。在Transformer模型中引入了self-Attention这一概念,Transformer的整个架构就是叠层的self-Attention和全连接层。具体的结构如下:
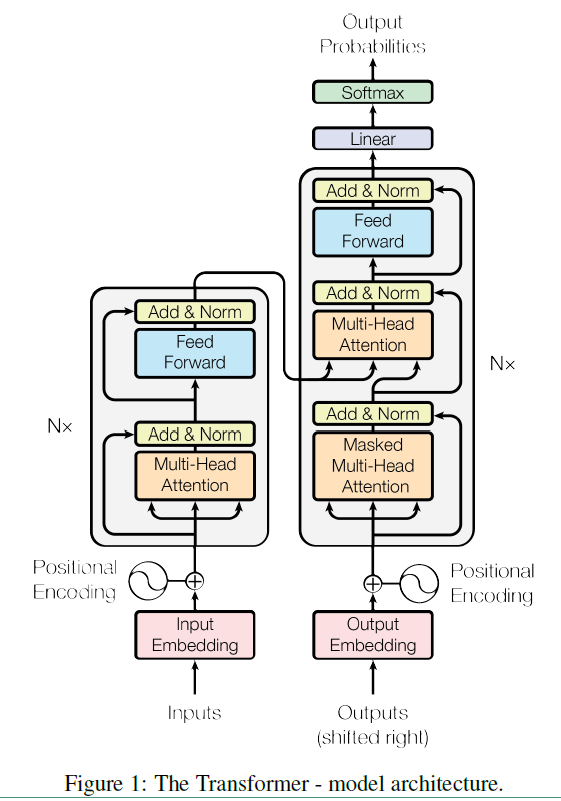
上面结构中的左半部分是Encoder,右半部分是Decoder。在详细介绍结构之前,先来看几个概念词:
self-Attention
在一般的Attention中,source和target中的内容是不一样的,也就是Query是不属于Key的。而self-Attention是发生在单个句子内的,它的Query是属于Key的,可以认为下面公式中
$ Attention(Query, source) = sum_{i=1}^{L_x} Similarity(Query, Key_i) * Value_i $
上面公式中Query = Key = Value。也就是说在序列内部做Attention,寻找序列内部的联系。
那么为什么要用self-Attention呢?它有什么优点:
1) 可以并行化处理,在计算self-Attention是不依赖于其他结果的。
2)计算复杂度低,self-Attention的计算复杂度是$n^2 d$,而RNN是$n d^2$,在这里$n$是指序列的长度,$d$是指词向量的维度,一般来说$d$的值是大于$n$的。
3)self-Attention可以很好的捕获全局信息,无论词的位置在哪,词之间的距离都是1,因为计算词之间的关系时是不依赖于其他词的。在大量的文献中表明,self-Attention的长距离信息捕捉能力和RNN相当,远远超过CNN(CNN主要是捕捉局部信息,当然可以通过增加深度来增大感受野,但实验表明即使感受野能涵盖整个句子,也无法较好的捕捉长距离的信息)。
Scaled dot-product attention
Scaled dot-product attention 的公式如下:
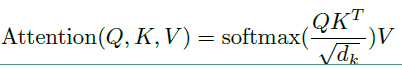
在上面公式中Q和K中的向量维度都是 $d_k$ ,V的向量维度是 $d_v$ ,实际上在self-Attention中,$d_k = d_v = d_wordEmbedding / numHeads$,为了方便将Attention的计算转化为矩阵运算,论文在这里采用了点积的形式求相似度。常见的计算方法除了点积还有MLP网络,但是点积能转化为矩阵运算,计算速度更快。然而点积的方法面临一个问题,当 $d_k$ 太大时,点积计算得到的内积会太大,这样会导致softmax的结果非0即1,因此引入了$sqrt{d_k}$ 来对内积进行缩放。
Multi-Head Attention
这是本文中首次提出的概念,这里的用法有点玄妙,但理解起来也很简单,其表达式如下:

表达式的计算如下:
1)假设现在头数为$h$,首先按照每一时序上的向量长度(如果是词向量的形式输入,可以理解为embedding size的值)等分成$h$份。
2)然后将上面等分后的$h$份数据分别通过不同的权重($W_i^Q, W_i^K, W_i^V$)映射得到新的Q, K, W的值。
3)将上述映射后的$h$份数据计算相应的Attention的值。
4)按照之前分割的形式重新拼接起来,再映射到原始的向量维度。就得到Multi-Head Attention的值。
在这里每一次映射时的矩阵都不相同,因此映射之后再计算也就会得到不一样的结果。其实认真来看Multi-Head Attention的机制有点类似与卷积中的多个卷积核,在卷积网络中,我们认为不同的卷积核会捕获不同的局部信息,在这里也是一样,我们认为Multi-Head Attention主要有两个作用:
1)增加了模型捕获不同位置信息的能力,如果你直接用映射前的Q, K, V计算,只能得到一个固定的权重概率分布,而这个概率分布会重点关注一个位置或个几个位置的信息,但是基于Multi-Head Attention的话,可以和更多的位置上的词关联起来。
2)因为在进行映射时不共享权值,因此映射后的子空间是不同的,认为不同的子空间涵盖的信息是不一样的,这样最后拼接的向量涵盖的信息会更广。
有实验证明,增加Mult-Head Attention的头数,是可以提高模型的长距离信息捕捉能力的。
Feed Forward 层
Feed Forward 层采用了全连接层加Relu函数实现,用公式可以表示为:
$ FFN(x) = Relu(xW_1 + b_1) W_2 + b_2$
其实关于在这里并不一定要用全连接层,也可以使用卷积层来实现。
Dropout 层
我们还可以在每个subLayers后面加上一个10%的Dropout层,则subLayers的输出可以写成:
$ LayerNorm(x + Dropout(Sublayer(x)))$
介绍到这里可以来看下我们整体的模型结构了。
Encoder
Encoder 是有N=6个layers层组成的,每一层包含了两个sub-layers。第一个sub-layer就是多头注意力层(multi-head attention layer),第二个就是一个简单的全连接层。在每个sub-layer层之间都用了残差连接,根据resNet,我们知道残差连接实际上是:
$H(x) = F(x) + x$
因此每个sub-layer的输出都是:
$ LayerNorm(x + Sublayer(x)) $
在这里LayerNorm中每个样本都有不同的均值和方差,不像BatchNormalization是整个batch共享均值和方差。
注意:每个Layer的输入和输出的维度是一致的。
Decoder
Decoder 同样是N=6个layers层组成的,但是这里的layer和Encoder不一样,这里的layer包含了三个sub-layers。第一个sub-layer就是多头自注意力层,也是计算输入的self-Attention,但是因为这是一个生成过程,因此在时刻 $t$ ,大于 $t$ 的时刻都没有结果,只有小于 $t$ 的时刻有结果,因此需要做masking,masking的作用就是防止在训练的时候使用未来的输出的单词。第二个sub-layer是对encoder的输入进行attention计算的,从这里可以看出Decoder的每一层都会对Encoder的输出做Multi Attention(这里的Attention就是普通的Attention,非self-Attention)。第三个sub-layer是全连接层。
从上面的分析来看Attention在模型中的应用有三个方面:
1)Encoder-Decoder Attention
在这里就和普通的Attention一样运用,query来自Decoder,key和value来自Encoder。
2)Encoder Attention
这里是self-Attention,在这里query,key,value都是来自于同一个地方
3)Decoder Attention
这里也是self-Attention,在这里的query,key,value也都是来自于同一个地方。但是在这里会引入masking。
Embedding and Softmax
和其他的序列传导模型一样,在这里的source,target的输入都会使用word embedding。也会用softmax来预测token
Positional Embedding
Positional Embedding 是一个很重要的东西,我们回过头来看上面的self-Attention,我们发现self-Attention能提取词与词之间的依赖关系,但是却不能提取词的绝对位置或者相对位置关系。如果将K,V的顺序打乱,获得的Attention的结果还是一样的。在NLP任务中词之间的顺序是很重要的,因此文章运用了Positional Embedding来保留词的信息,将每个位置编号,然后每个编号对应这一向量,最后将该向量和词向量相加,这样就给每个词引入了一定的位置信息。
在论文中使用不同频率的正弦和余弦函数来生成位置向量,表达式如下:
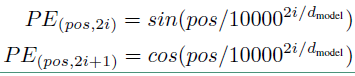
位置向量的维度和word embedding的一致。上面公式中 $pos$ 表示序列中词的位置,$i$ 表示位置向量中每个值的维度,也就是说$ i < d_{model}$。通过上面公式计算出每一个位置的位置向量。位置向量是可以被训练的值,而且用上面的公式计算的位置向量并不是绝对的,你也可以用其他的方法求位置向量。
参考文献:
深度学习中的注意力机制(2017版)
《Attention is All You Need》浅读(简介+代码)