第一个推广: 在生成树计数问题中,其实我们做了这样一个假设,就是每条边的权值是1。我们再来看下这个公式

对于关联矩阵B来说(对于一个n个顶点m条边的无向图G,它的关联矩阵B是一个n*m的矩阵。对于第i条边e[i]=(u,v),那么B[u][i]和B[v][i]中一个是1,一个是-1,第i列其他值为0),我们可以这样看,对于顶点(u,v) 之间若有边 e[x]=(u,v),那么B[u][x]=1,B[v][x]=-1,x列其他值为0。那么,现在我们设边(u,v)的权值为w(我们这里认为w非负,没有边的时候w=0),那么其实B满足下面的式子
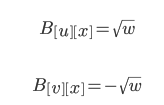
那么按照这个样子,$det(C_{r})$它计算出的是

其中

最后对于

也能构造出一个上三角矩阵,对角线分别是到它父节点的边的权值。
第二个推广:我们来求带权无向图的最小生成树的个数。如果图的权值都是相同的,那么直接使用matrix-tree定理计算即可。对于不是这样情况的,我们可以这样解决。首先将边权升序排序,这样权值相等的边就排到了一起。然后,相等权值的边划分为一组。我们按照组一组一组处理。
在这里有这样一个性质,设在某一种最小生成树中边权为w的边使用了x条,那么在所有类型的最小生成树中,边权为w的边都必然使用了x条,并且这x条边加上之前权值小于w的边中选出的一些边加入后图的联通状态不变。首先我们来证明联通状态不变。首先,我们假设在权值为w的边处理之前,处理完权值小于w的边之后,形成的联通块数为c1,加入权值为w的x条边之后联通块数为c2,显然c2=c1-x。那么不管权值为w的边你选多少条如何选,之后联通块数都不会比c2更小了,要是更小,说明我们c2求错了。要是比c2大,那么这不是最优的情况,因为对于某两个未联通的块,现在让他俩联通一定比之后让他俩联通优,因为后面的权值越来越大。接着我们证明,使用的边的数量一定是x,这也很显然,c1,c2都是固定的,联通块数减少了c1-c2,所以一定用了这么多边,不能多也不能少。
有了这个性质,我们对于每个阶段,我们将这个阶段之前的联通到一起的点看做一个点,那么权值为w的所有边加入后,就成了一些联通块,每个联通块内边的权值都一样,所以可以使用matrix-tree 定理搞一次,所有的联通块的乘起来即可。而每个阶段是独立的,乘起来就是最后答案。