A Visual Exploration of Gaussian Processes
地址:https://www.jgoertler.com/visual-exploration-gaussian-processes/
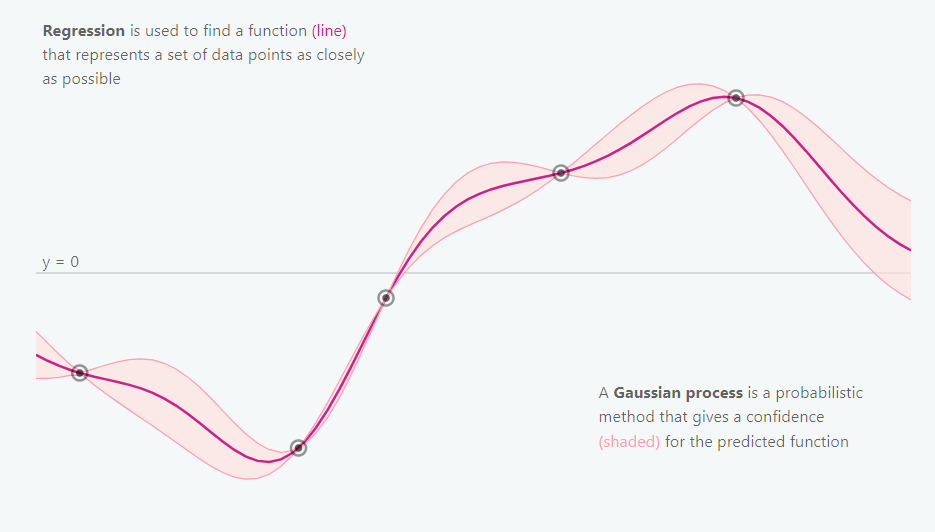
高斯过程是一种非参数建模方法,试图寻找与观测数据点相一致的所有可能函数的分布。
与所有贝叶斯方法相同,高斯过程从一个先验分布开始,并采用观测数据对其更新,从而得到函数的后验分布。

非参数方法并不是没有参数,而是有无穷多个参数(即,我们考虑的是函数的分布,可以含有任意多个参数。)。
核心思想
高斯过程从一个函数的先验分布开始,并采用观测数据对其更新,从而得到函数的后验分布。
如何表示函数的分布?听起来有些困难!事实证明,我们只需要在一个有限但任意的点集上(如,x1, x2, ..., xN)定义一个分布。
高斯过程假设 p(f(x1),…,f(xN)) 是一个多变量联合高斯分布, 均值向量为μ(x) ,协方差矩阵为∑(x) (矩阵元素为∑ij=k(xi,xj))。
协方差矩阵通过一个被称为核函数K的东西进行计算。核函数是正定的,其形式有很多(参考Rasmussen and Williams book.)。
核函数应保证计算出的协方差矩阵满足对称半正定的性质。
其核心思想为,如果xi和xj被核函数认为是相似的,那么我们期望函数在这些点上的输出值也是相似的。
GPs的数学关键是多变量高斯分布。

我们是如何得出后验分布的?
GPs的数学关键是多变量高斯分布。如果我们知道多变量的联合概率密度分布,在给定其他变量的情况下,有可能得到其中一个变量的条件概率,
这就是在gp中,我们如何从先验分布和我们的观测点中得出后验分布。



一个例子
import numpy as np import matplotlib.pyplot as pl # Test data n = 50 Xtest = np.linspace(-5, 5, n).reshape(-1,1) # Define the kernel function def kernel(a, b, param): sqdist = np.sum(a**2,1).reshape(-1,1) + np.sum(b**2,1) - 2*np.dot(a, b.T) return np.exp(-.5 * (1/param) * sqdist) param = 0.1 K_ss = kernel(Xtest, Xtest, param) # Get cholesky decomposition (square root) of the # covariance matrix L = np.linalg.cholesky(K_ss + 1e-15*np.eye(n)) # Sample 3 sets of standard normals for our test points, # multiply them by the square root of the covariance matrix f_prior = np.dot(L, np.random.normal(size=(n,3))) # Now let's plot the 3 sampled functions. pl.plot(Xtest, f_prior) pl.axis([-5, 5, -3, 3]) pl.title('Three samples from the GP prior') pl.show()
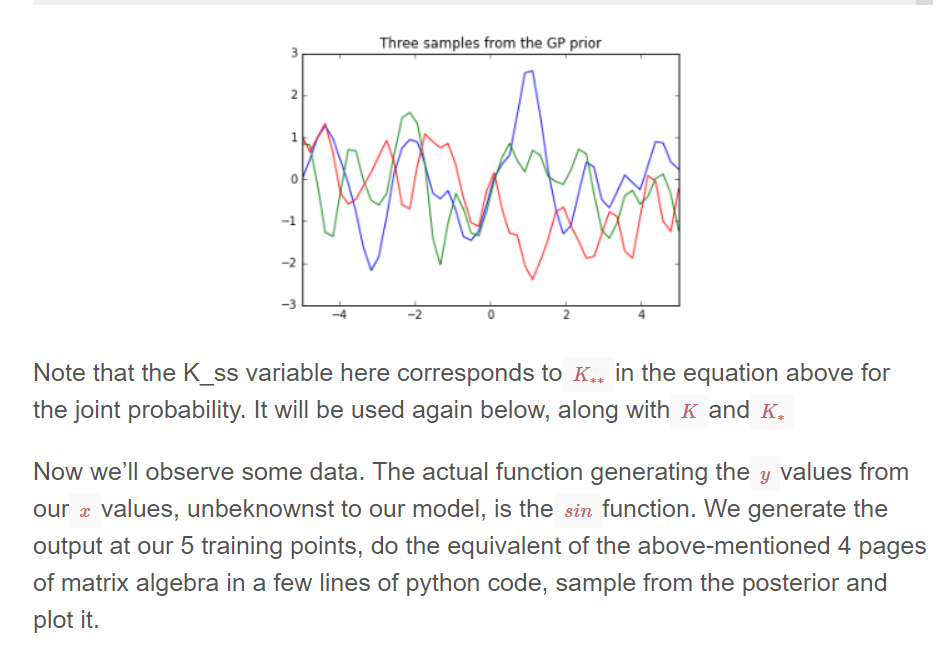
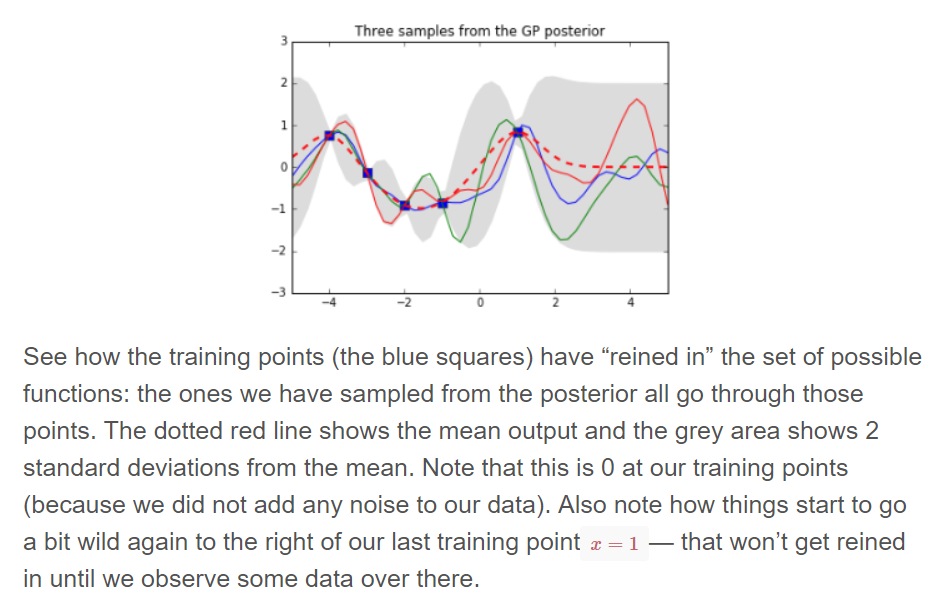
# Noiseless training data Xtrain = np.array([-4, -3, -2, -1, 1]).reshape(5,1) ytrain = np.sin(Xtrain) # Apply the kernel function to our training points K = kernel(Xtrain, Xtrain, param) L = np.linalg.cholesky(K + 0.00005*np.eye(len(Xtrain))) # Compute the mean at our test points. K_s = kernel(Xtrain, Xtest, param) Lk = np.linalg.solve(L, K_s) mu = np.dot(Lk.T, np.linalg.solve(L, ytrain)).reshape((n,)) # Compute the standard deviation so we can plot it s2 = np.diag(K_ss) - np.sum(Lk**2, axis=0) stdv = np.sqrt(s2) # Draw samples from the posterior at our test points. L = np.linalg.cholesky(K_ss + 1e-6*np.eye(n) - np.dot(Lk.T, Lk)) f_post = mu.reshape(-1,1) + np.dot(L, np.random.normal(size=(n,3))) pl.plot(Xtrain, ytrain, 'bs', ms=8) pl.plot(Xtest, f_post) pl.gca().fill_between(Xtest.flat, mu-2*stdv, mu+2*stdv, color="#dddddd") pl.plot(Xtest, mu, 'r--', lw=2) pl.axis([-5, 5, -3, 3]) pl.title('Three samples from the GP posterior') pl.show()
Further Reading
The following blog posts offer more interactive visualizations and further reading material on the topic of Gaussian processes:
- Gaussian process regression demo by Tomi Peltola
- Gaussian Processes for Dummies by Katherine Bailey (写的很详细)
- Intuition behind Gaussian Processes by Mike McCourt
- Fitting Gaussian Process Models in Python by Chris Fonnesbeck
If you want more of a hands-on experience, there are also many Python notebooks available:
- Fitting Gaussian Process Models in Python by Chris Fonnesbeck
- Gaussian process lecture by Andreas Damianou