Logistic 回归(实际上是一种分类算法)
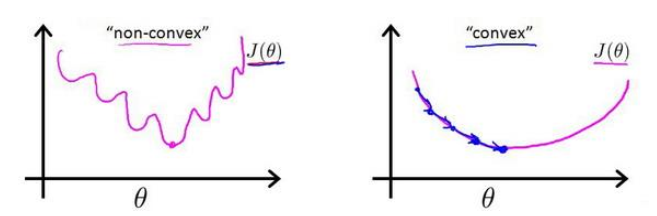
代价函数的选择:在线性回归模型时,选取所有模型误差的平方和最为代价函数。但是当我们将$h_\theta(x)=\frac{1}{1+e^{-{\theta}^T}}$代入定义了的代价的代价函数中时,我们得到的代价函数将是一个非凸函数。(实际上继续误差平方和作为代价函数也可以)
这意味着我们的代价函数有许多局部最小值,这将影响梯度下降算法寻找全局最小值。
重新定义的代价函数:
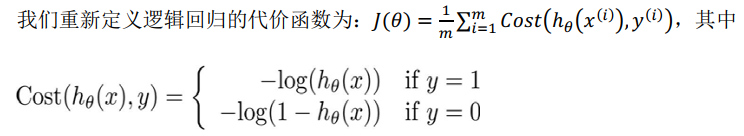
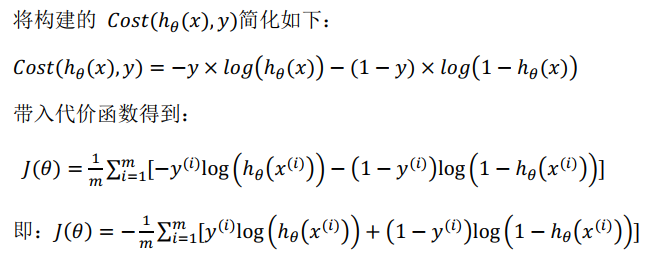
梯度下降的计算过程(假设函数中加入了sigma函数,且代价函数的定义也与之前不一样):

梯度下降的例子:(便于梯度湘江更新过程的理解)

tips:自己编写梯度下降法进行$\theta$更新是一种选择,但是也可以调用matlab,python中的相关库函数进行调试
过拟合和欠拟合:
过拟合:导致模型的泛化能力过差,当特征很多但是训练的数据过少,就会出现过拟合。想象一个极端例子:有800个特征,则需要800个权重(忽略偏置),若值若只有500个数据,则就不能完美的解除每个特征的权重。800个权重,数据只有900个的情况也差不多。
过拟合解决方法:1、舍弃一些特征信息 (缺点是会损失一部分信息) 2、进行正则化,保留所有的特征,但是减少参数的大小( magnitude)
正则化:
对于简单的拟合函数$h_\theta=\theta_0+\theta_1x_1+\theta_2x_2^2+\theta_3x_3^3+theta_4x_4^4$(其中没有加上费线性激活g(z),不影响表达),实际上就是高次项使得最后是过拟合。则我们要做的就是使高次项的系数$\theta_3 ,\theta_4$在一定程度上变小,其方法如下:在代价函数后面增加一个惩罚项,如这里的$1000\theta_3^2+10000\theta_4^2$(随便加,只要保证J随着增加项的增大而非常明显的增大即可)。此时,若想要最小化代价函数,则显然$\theta_3 , \theta_4$会被压得很低,接近于0,则高次项系数接近于0,最后结果仍然接近于2次(由$x^2$次数得到)
实际上,若对所有的项都进行这样的“惩罚”,则最后得到的拟合结果会很平滑,且不容易过拟合。

因为在实际中,不知道应该缩小哪些参数,所以就会的到$J(\theta)=\frac{1}{2m}[\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^2+\lambda \sum_{i=1}^n\theta_j^2]$
tis:这里的后一项是正则化项(其中$、lambda$为正则化参数),但不是从$i=0$开始的,并没有给$\theta_0$增加惩罚项,这是约定俗成,但是加上也可以。
tips:对于正则化参数$\lambda$,设置过大会造成对参数$\theta$抑制过大,造成欠拟合;反之,则欠拟合。正则化参数的选取需格外注意。当然,也有自动选择正则化参数的方法,这节课老师没讲,自行百度

tips:按照普通的梯度下降,则没有$1-\alpha\frac{\lambda}{m}$这一项,而这一项一般都是微微小于1的

还是有点不懂,之后再看看
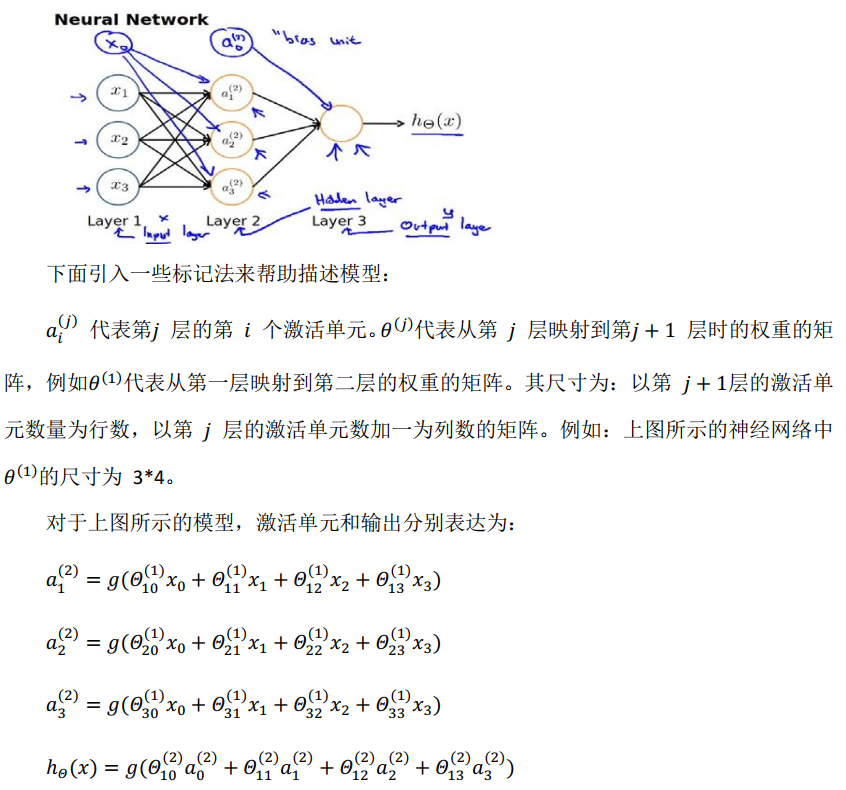
神经网络:
tips:需要注意的是图中在$x_1$上面填上了一个$x_0$,这个代表的是偏置,这个偏置会通过与$\theta_0$相乘的方式达到和之前偏置一样的效果(其中$\theta$全是1)
tips:而且,下面公式的上下标也有考虑的进行了反写 如$\theta_{10}^{(1)}$ $(1)$代表了这是第一层的参数,下标$_{10}$代表的是从第0个神经元连接到第一个神经元。将两者结合,则表示,第一层的权重从前一层的第0个神经元接收到结果并进行加权。
向量化表(以计算第二层的值为例):
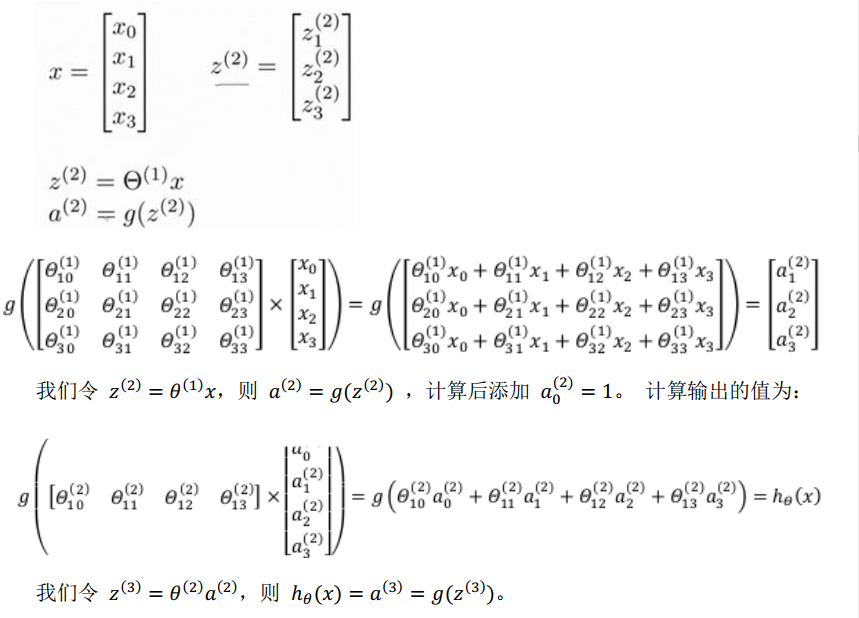
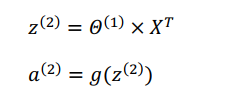
下图的理解 :第1层的编号为2的神经元(实际上是第三个)映射到下一层(第2层)的编号为3的神经元(实际上是第四个),其中$x_2$是第1层编号为2的神经元的输出($x_2$的编号是二,实际上由于人为加入偏置,他实际是第三个神经元的输出)【注意下标的反写】
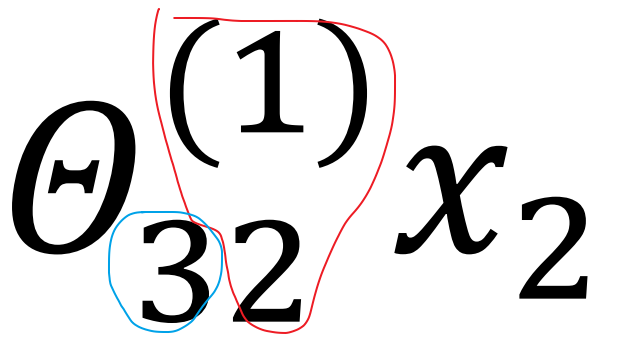
神经网络的代价函数
