二分搜索（2、Yougth的最大化，无限逼近最大值)

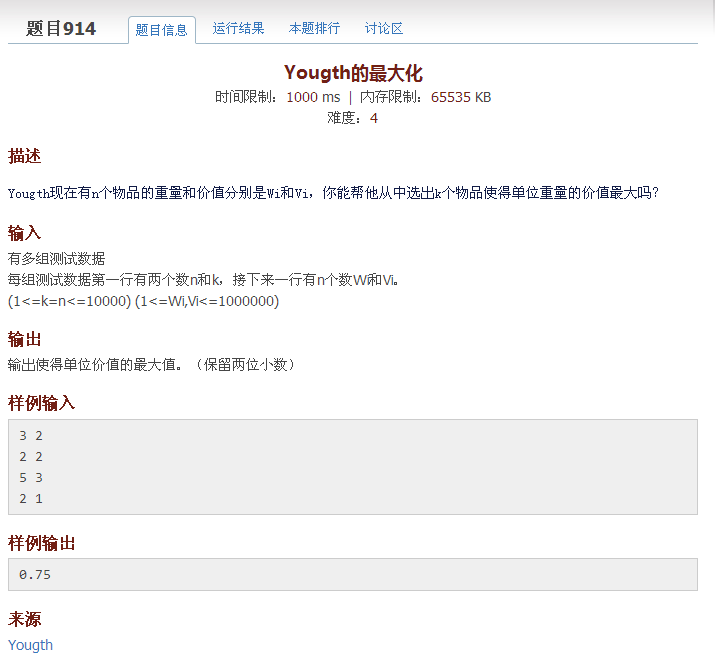
条件C(x):=可以选择是单位重量的价值不小于x,则该问题就变成了满足C(x)的最大的x,那么怎么判断C(x)是否可行呢？假设我们选了某个物品的集合S，那么它们的单位重量价值是：

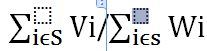
因此就变成了判断是否存在s满足下面条件：

把这个不等是进行变形就得到

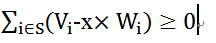
//#define LOCAL
#include<cstdio>
//#include<iostream>注意引入头文件，编译时候需要连接，是费内存的，如果不需要尽量不要引入
#include<algorithm>
int const MAX_N=10010;
int const MAX_M=100;
double const INF=10000000.0;
int W[MAX_N],V[MAX_N],n,k;
double Y[MAX_N];
void readdate()
{
    for(int i=0;i<n;i++)
    {
        scanf("%d%d",&W[i],&V[i]);
    }
}
bool C(double x)
{
    for(int i=0;i<n;i++)
    {
        Y[i]=V[i]-x*W[i];
    }
    std::sort(Y,Y+n);
    //计算Y数组中从大到小前k个数的和
    double sum=0.0;
    for(int i=0;i<k;i++)
    {
        sum+=Y[n-i-1];
    } 
    return sum>=0;
}
void solve()
{
    double lb=0.0,ub=INF;
    for(int i=0;i<MAX_M;i++)
    {
        double mid=(lb+ub)/2;
        if(C(mid)) lb=mid;
        else ub=mid;
    }
    printf("%.2f
",ub);
}
int main()
{
#ifdef LOCAL
    freopen("914.in","r",stdin);
    freopen("914.out","w",stdout);
#endif
    ;
    while(~scanf("%d%d",&n,&k))
    {
        readdate();
        solve();
    }
    return 0;
}