牛牛的DRB迷宫I
链接:https://ac.nowcoder.com/acm/contest/3004/A
来源:牛客网
题目描述
牛牛有一个n*m的迷宫,对于迷宫中的每个格子都为'R','D','B'三种类型之一,'R'表示处于当前的格子时只能往右边走'D'表示处于当前的格子时只能往下边走,而'B'表示向右向下均可以走。
我们认为迷宫最左上角的坐标为(1,1),迷宫右下角的坐标为(n,m),除了每个格子有向右移动以及向下移动的限制之外,你也不能够走出迷宫的边界。
牛牛现在想要知道从左上角走到右下角不同种类的走法共有多少种,请你告诉牛牛从(1,1)节点移动到(n,m)节点共有多少种不同的移动序列,请你输出方案数对109+7取余数后的结果。
我们认为两个移动序列是不同的,当且仅当移动序列的长度不同,或者在某一步中采取了不同的移动方式。
输入描述:
第一行输入两个正整数n,m(1≤n,m≤50)表示迷宫的大小是n行m列。
接下来n行,每行输入一个长度为m的字符串,字符串中仅包含大写字母'D','R','B'。
输出描述:
输出一行一个整数,表示方案数对109+7取余数后的结果。
输入
5 5 RBBBR BBBBB BBBDB BDBBB RBBBB
输出
25
这个题比较简单,是经典的走格子DP(棋盘型DP)。时空复杂度O(nm)
1 #include <stdio.h> 2 #include <string.h> 3 #include <iostream> 4 #include <string> 5 #include <math.h> 6 #include <algorithm> 7 #include <vector> 8 #include <stack> 9 #include <queue> 10 #include <set> 11 #include <map> 12 #include <sstream> 13 const int INF=0x3f3f3f3f; 14 typedef long long LL; 15 const int mod=1e9+7; 16 const int maxn=1e5+10; 17 using namespace std; 18 19 char G[55][55]; 20 LL dp[55][55]; 21 22 int main() 23 { 24 #ifdef DEBUG 25 freopen("sample.txt","r",stdin); 26 #endif 27 28 int n,m; 29 scanf("%d %d",&n,&m); 30 for(int i=1;i<=n;i++) 31 scanf("%s",G[i]+1); 32 dp[1][0]=1; 33 for(int i=1;i<=n;i++) 34 { 35 for(int j=1;j<=m;j++) 36 { 37 if(G[i][j-1]!='D') dp[i][j]=(dp[i][j]+dp[i][j-1])%mod; 38 if(G[i-1][j]!='R') dp[i][j]=(dp[i][j]+dp[i-1][j])%mod; 39 } 40 } 41 printf("%lld ",dp[n][m]); 42 43 return 0; 44 }
牛牛的DRB迷宫II
链接:https://ac.nowcoder.com/acm/contest/3004/B
来源:牛客网
题目描述
牛牛有一个n*m的迷宫,对于迷宫中的每个格子都为'R','D','B'三种类型之一,'R'表示处于当前的格子时只能往右边走'D'表示处于当前的格子时只能往下边走,而'B'表示向右向下均可以走。
我们认为迷宫最左上角的坐标为(1,1),迷宫右下角的坐标为(n,m),除了每个格子有向右移动以及向下移动的限制之外,你也不能够走出迷宫的边界。
牛牛现在请你设计迷宫,但是要求你设计的迷宫符合他的要求,他要求你设计的迷宫从(1,1)节点移动到(n,m)节点不同的移动序列种类数目≡k(mod109+7)。
请你构造出符合条件的DRB迷宫,但是要求你输出的迷宫的大小不超过50*50,具体输出格式见输出描述及样例。
如果存在多解你可以构造任意符合条件的迷宫,反之如果无解,请输出一行一个字符串"No solution"。
输入描述:
仅一个整数k,你需要构造一个DRB迷宫符合从左上走到右下的方案数≡k(mod109+7)。
输出描述:
请你构造出符合条件的DRB迷宫,但是要求你输出的迷宫的大小不超过50*50。
输入
25
输出
5 5 RBBBR BBBBB BBBDB BDBBB RBBBB
说明
样例为《牛牛的DRB迷宫I》中的样例反过来。
备注:
构造A题中的迷宫,要求方案数整好等于给定的k,可以构造一个二进制编码器,斜对角线上的方案数恰好是1,2,4,8,16,32...,用二进制可以拼出所有的数字,所以一定能造的出来。
题解的图是这样的,即主对角线上的格子都为B,它的上面点为D,下面点为R。那么一开始这样的初始图的方案数为2n-1个。
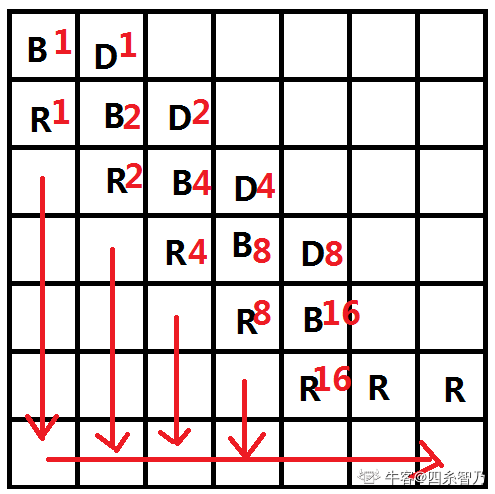
10^9+7的二进制是30位,开G[32][30],每一列相当于一个二进制位,前面31行是二进制编码器,相当于多加了一行来在判断该二进制位是否为1后通向G[32][30]
前31行:

如果k=25,输出为:

1 #include <stdio.h> 2 #include <string.h> 3 #include <iostream> 4 #include <string> 5 #include <math.h> 6 #include <algorithm> 7 #include <vector> 8 #include <stack> 9 #include <queue> 10 #include <set> 11 #include <map> 12 #include <sstream> 13 const int INF=0x3f3f3f3f; 14 typedef long long LL; 15 const int mod=1e9+7; 16 const int maxn=1e5+10; 17 using namespace std; 18 19 char G[55][55]; 20 21 int main() 22 { 23 #ifdef DEBUG 24 freopen("sample.txt","r",stdin); 25 #endif 26 27 int k; 28 scanf("%d",&k); 29 for(int i=1;i<=32-1;i++)//前面31行相当于二进制编码器 30 { 31 for(int j=1;j<=30;j++) 32 { 33 if(j<i-1) G[i][j]='D';//左方为D 34 else if(j<i+2) G[i][j]='B';//i和其左右为B 35 else G[i][j]='R';//右方为R 36 } 37 } 38 for(int i=1;i<=30;i++) 39 { 40 if( !(k&( 1<<(i-1) )) ) G[i+1][i]='R';//封路 41 G[32][i]='R';//加上最后一行 42 } 43 printf("%d %d ",32,30); 44 for(int i=1;i<=32;i++) 45 printf("%s ",G[i]+1); 46 47 return 0; 48 }
-