Codeforces Round #385 (Div. 2) A,B,C 暴力，模拟，并查集

A. Hongcow Learns the Cyclic Shift

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Hongcow is learning to spell! One day, his teacher gives him a word that he needs to learn to spell. Being a dutiful student, he immediately learns how to spell the word.

Hongcow has decided to try to make new words from this one. He starts by taking the word he just learned how to spell, and moves the last character of the word to the beginning of the word. He calls this a cyclic shift. He can apply cyclic shift many times. For example, consecutively applying cyclic shift operation to the word "abracadabra" Hongcow will get words "aabracadabr", "raabracadab" and so on.

Hongcow is now wondering how many distinct words he can generate by doing the cyclic shift arbitrarily many times. The initial string is also counted.

Input

The first line of input will be a single string s (1 ≤ |s| ≤ 50), the word Hongcow initially learns how to spell. The string s consists only of lowercase English letters ('a'–'z').

Output

Output a single integer equal to the number of distinct strings that Hongcow can obtain by applying the cyclic shift arbitrarily many times to the given string.

Examples

input

abcd

output

4

input

bbb

output

1

input

yzyz

output

2

Note

For the first sample, the strings Hongcow can generate are "abcd", "dabc", "cdab", and "bcda".

For the second sample, no matter how many times Hongcow does the cyclic shift, Hongcow can only generate "bbb".

For the third sample, the two strings Hongcow can generate are "yzyz" and "zyzy".

题意：给你一个字符串，字符串可以将最后一个放第一个，其余全部往后推，问最多有多少个不同的字符串；

思路：暴力枚举起始点，字符串hash；

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
#define eps 1e-14
const int N=1e5+10,M=1e6+10,inf=1e9+10;
const ll INF=1e18+10,mod=2147493647;
char a[N];
map<string,int>m;
int main()
{
    scanf("%s",&a);
    int n=strlen(a);
    int ans=0;
    for(int i=0;i<n;i++)
    {
        string aa="";
        for(int j=i;j<n;j++)
            aa+=a[j];
        for(int j=0;j<i;j++)
            aa+=a[j];
        if(!m[aa])
            ans++;
        m[aa]=1;
    }
    printf("%d
",ans);
    return 0;
}

B. Hongcow Solves A Puzzle

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Hongcow likes solving puzzles.

One day, Hongcow finds two identical puzzle pieces, with the instructions "make a rectangle" next to them. The pieces can be described by an n by m grid of characters, where the character 'X' denotes a part of the puzzle and '.' denotes an empty part of the grid. It is guaranteed that the puzzle pieces are one 4-connected piece. See the input format and samples for the exact details on how a jigsaw piece will be specified.

The puzzle pieces are very heavy, so Hongcow cannot rotate or flip the puzzle pieces. However, he is allowed to move them in any directions. The puzzle pieces also cannot overlap.

You are given as input the description of one of the pieces. Determine if it is possible to make a rectangle from two identical copies of the given input. The rectangle should be solid, i.e. there should be no empty holes inside it or on its border. Keep in mind that Hongcow is not allowed to flip or rotate pieces and they cannot overlap, i.e. no two 'X' from different pieces can share the same position.

Input

The first line of input will contain two integers n and m (1 ≤ n, m ≤ 500), the dimensions of the puzzle piece.

The next n lines will describe the jigsaw piece. Each line will have length m and will consist of characters '.' and 'X' only. 'X' corresponds to a part of the puzzle piece, '.' is an empty space.

It is guaranteed there is at least one 'X' character in the input and that the 'X' characters form a 4-connected region.

Output

Output "YES" if it is possible for Hongcow to make a rectangle. Output "NO" otherwise.

Examples

input

2 3
XXX
XXX

output

YES

input

2 2
.X
XX

output

NO

input

5 5
.....
..X..
.....
.....
.....

output

YES

Note

For the first sample, one example of a rectangle we can form is as follows

111222
111222

For the second sample, it is impossible to put two of those pieces without rotating or flipping to form a rectangle.

In the third sample, we can shift the first tile by one to the right, and then compose the following rectangle:

.....
..XX.
.....
.....
.....

题意：问你是否只有一个矩形；

思路：找到最上面左边的点和最下面右边为矩阵左右边界，判断是否问矩形，再求矩形外面是否有X；

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
#define eps 1e-14
const int N=1e3+10,M=1e6+10,inf=1e9+10;
const ll INF=1e18+10,mod=2147493647;
char mp[N][N];
int stx,sty;
int enx,eny;
int n,m;
void checks()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            if(mp[i][j]=='X')
            {
                stx=i;
                sty=j;
                return;
            }
        }
    }
}
void checke()
{
    for(int i=n;i>=1;i--)
    {
        for(int j=m;j>=1;j--)
        {
            if(mp[i][j]=='X')
            {
                enx=i;
                eny=j;
                return;
            }
        }
    }
}
int check(int s,int ss,int e,int ee)
{
    int sum=0;
    for(int i=s;i<=e;i++)
    {
        for(int j=ss;j<=ee;j++)
        {
            if(mp[i][j]!='X')
                return -1;
            sum++;
        }
    }
    return sum;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%s",mp[i]+1);
    }
    checks();
    checke();
    if(!stx||!enx)
        return puts("NO
");
    int no=check(stx,sty,enx,eny),ans=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
            if(mp[i][j]=='X')
            ans++;
    }
    if(ans==no)
        printf("YES
");
    else
        printf("NO
");
    return 0;
}

C. Hongcow Builds A Nation

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Hongcow is ruler of the world. As ruler of the world, he wants to make it easier for people to travel by road within their own countries.

The world can be modeled as an undirected graph with n nodes and m edges. k of the nodes are home to the governments of the kcountries that make up the world.

There is at most one edge connecting any two nodes and no edge connects a node to itself. Furthermore, for any two nodes corresponding to governments, there is no path between those two nodes. Any graph that satisfies all of these conditions is stable.

Hongcow wants to add as many edges as possible to the graph while keeping it stable. Determine the maximum number of edges Hongcow can add.

Input

The first line of input will contain three integers n, m and k (1 ≤ n ≤ 1 000, 0 ≤ m ≤ 100 000, 1 ≤ k ≤ n) — the number of vertices and edges in the graph, and the number of vertices that are homes of the government.

The next line of input will contain k integers c1, c2, ..., ck (1 ≤ ci ≤ n). These integers will be pairwise distinct and denote the nodes that are home to the governments in this world.

The following m lines of input will contain two integers ui and vi (1 ≤ ui, vi ≤ n). This denotes an undirected edge between nodes ui andvi.

It is guaranteed that the graph described by the input is stable.

Output

Output a single integer, the maximum number of edges Hongcow can add to the graph while keeping it stable.

Examples

input

4 1 2
1 3
1 2

output

2

input

3 3 1
2
1 2
1 3
2 3

output

0

Note

For the first sample test, the graph looks like this:

Vertices 1 and 3 are special. The optimal solution is to connect vertex 4 to vertices 1 and 2. This adds a total of 2 edges. We cannot add any more edges, since vertices 1 and 3 cannot have any path between them.

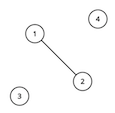
For the second sample test, the graph looks like this:

We cannot add any more edges to this graph. Note that we are not allowed to add self-loops, and the graph must be simple.

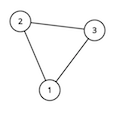
 题意：给你一个无向图，n个村庄，m条边，k个政府，不能让两个政府联通，问最多能加多少条边；

思路：首先并查集一下，找到一个最大的集合，将无政府的点，加进去，然后将每个集合所有点有相互连接即可；

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
#define eps 1e-14
const int N=1e5+10,M=1e6+10,inf=1e9+10;
const ll INF=1e18+10,mod=2147493647;
int fa[N],si[N];
int flag[N];
int Find(int x)
{
    return x==fa[x]?x:fa[x]=Find(fa[x]);
}
void update(int x,int y)
{
    int u=Find(x);
    int v=Find(y);
    if(u!=v)
    {
        if(flag[u])
        {
            fa[v]=u;
            si[u]+=si[v];
        }
        else
        {
            fa[u]=v;
            si[v]+=si[u];
        }
    }
}
int u[N],v[N];
int main()
{
    int n,m,k;
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=k;i++)
    {
        int x;
        scanf("%d",&x);
        flag[x]=1;
    }
    for(int i=1;i<=n;i++)
    {
        fa[i]=i;
        si[i]=1;
    }
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&u[i],&v[i]);
        update(u[i],v[i]);
    }
    int ma=0,pos;
    for(int i=1;i<=n;i++)
    {
        if(flag[i])
        {
            if(si[i]>ma)
            {
                ma=si[i];
                pos=i;
            }
        }
    }
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        int x=Find(i);
        if(x==pos||!flag[x])
            ans++;
    }
    //cout<<ans<<endl;
    ans=ans*(ans-1)/2;
    for(int i=1;i<=n;i++)
    {
        int x=Find(i);
        if(x!=pos&&flag[x])
            ans+=si[x]*(si[x]-1)/2;
        flag[x]=0;
    }
    ans-=m;
    printf("%d
",ans);
    return 0;
}