Mad scientist Mike is building a time machine in his spare time. To finish the work, he needs a resistor with a certain resistance value.
However, all Mike has is lots of identical resistors with unit resistance R0 = 1. Elements with other resistance can be constructed from these resistors. In this problem, we will consider the following as elements:
- one resistor;
- an element and one resistor plugged in sequence;
- an element and one resistor plugged in parallel.
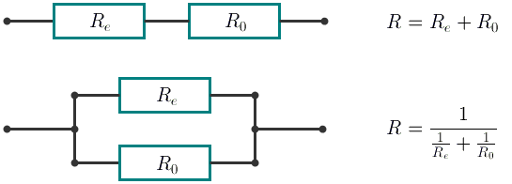
With the consecutive connection the resistance of the new element equals R = Re + R0. With the parallel connection the resistance of the new element equals 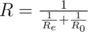 . In this case Re equals the resistance of the element being connected.
. In this case Re equals the resistance of the element being connected.
Mike needs to assemble an element with a resistance equal to the fraction  . Determine the smallest possible number of resistors he needs to make such an element.
. Determine the smallest possible number of resistors he needs to make such an element.
The single input line contains two space-separated integers a and b (1 ≤ a, b ≤ 1018). It is guaranteed that the fraction  is irreducible. It is guaranteed that a solution always exists.
is irreducible. It is guaranteed that a solution always exists.
Print a single number — the answer to the problem.
Please do not use the %lld specifier to read or write 64-bit integers in С++. It is recommended to use the cin, cout streams or the%I64d specifier.
1 1
1
3 2
3
199 200
200
In the first sample, one resistor is enough.
In the second sample one can connect the resistors in parallel, take the resulting element and connect it to a third resistor consecutively. Then, we get an element with resistance 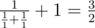 . We cannot make this element using two resistors.
. We cannot make this element using two resistors.
题意:要得到a/b的电阻最小需要多少个电阻;(注意:每次只能串联一个或者并联一个);
思路:每次串联一个得到(a+b)/a,并联一个得到a/(a+b);
#include<bits/stdc++.h> using namespace std; #define ll __int64 #define mod 1000000007 #define inf 100000000000005 #define MAXN 10000010 //#pragma comment(linker, "/STACK:102400000,102400000") int main() { ll x,y,z,i,t; scanf("%I64d%I64d",&x,&y); ll ans=0; while(1) { if(x>y) { ans+=x/y; x%=y; if(x==0) break; } else if(x<y) { z=x; x=y-x; y=z; ans++; } else { ans+=1; break; } } cout<<ans<<endl; return 0; }