571B. Minimization(Codeforces Round #317)

B. Minimization

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You've got array A, consisting of n integers and a positive integer k. Array A is indexed by integers from 1 to n.

You need to permute the array elements so that value

became minimal possible. In particular, it is allowed not to change order of elements at all.

Input

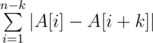
The first line contains two integers n, k (2 ≤ n ≤ 3·105, 1 ≤ k ≤ min(5000, n - 1)).

The second line contains n integers A[1], A[2], ..., A[n] ( - 109 ≤ A[i] ≤ 109), separate by spaces — elements of the array A.

Output

Print the minimum possible value of the sum described in the statement.

Sample test(s)

input

3 2
1 2 4

output

1

input

5 2
3 -5 3 -5 3

output

0

input

6 3
4 3 4 3 2 5

output

3

Note

In the first test one of the optimal permutations is 1 4 2.

In the second test the initial order is optimal.

In the third test one of the optimal permutations is 2 3 4 4 3 5.

解题思路：

      将数组分成k组，各自是i,i+k,i+2*k,i+3*k...(1<=i<=k),有x=n%k个组元素个数是n/k+1个，问题就转化为k组内

相邻元素差值的和的最小值，这时就须要对数组进行排序。仅仅有每组内的元素都是有序的，每组内的相邻元素的

差值才会最小，接着就是在k组内分x组长度为n/k+1，这时就须要dp，dp[i][j]。i是分了i组。j组长度是n/k+1;dp方

程为dp[i][j]=max(dp[i-1][j]+dp[i-1][j-1])+(a[i*n/k+j+1]-a[i*n/k+j])，ans=a[n]-a[1]-dp[k][x],a[i*n/k+j+1]-a[i*n/k+j]是要

从分第i组是,第i组的第1个元素与第i-1组的最后一个元素的差值。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=500000+100;
int a[maxn];
int s[maxn];
int bbs(int x)
{
    if(x<0)
    return -x;
    return x;
}
int dp[5500][5500];
int main()
{
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++)
    scanf("%d",&a[i]);
    sort(a+1,a+n+1);
    memset(dp,-1,sizeof(dp));
    int sum=a[n]-a[1];
    int q=n/k;
    int x=n%k;
    dp[0][0]=0;
    for(int i=1;i<=k;i++)
    {
        for(int j=0;j<=x;j++)
        {
            int df;
            if(j==0)
            df=dp[i-1][j];
            else
            df=max(dp[i-1][j],dp[i-1][j-1]);
            if(df<0)
            continue;
            if(i==k&&j==x)
            dp[i][j]=df;
            else
            dp[i][j]=df+a[i*q+j+1]-a[i*q+j];
        }
    }
    int ans=sum-dp[k][x];
    cout<<ans<<endl;
    return 0;
}