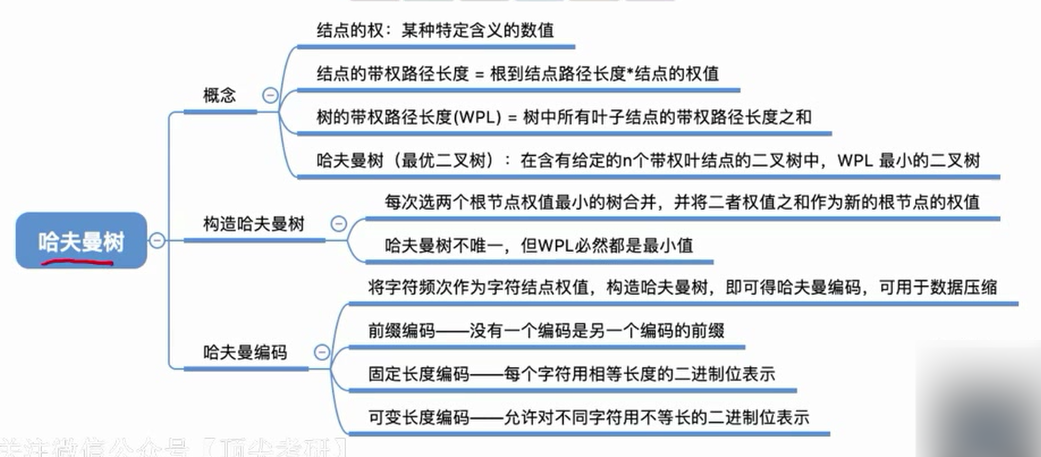
哈夫曼树
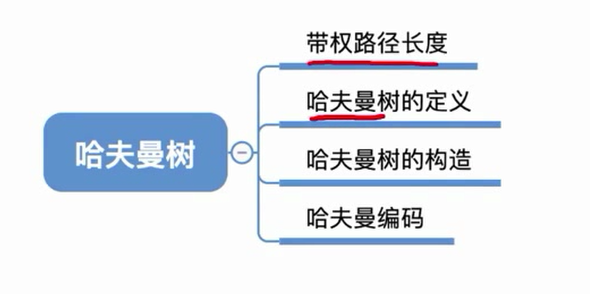
重点:构造哈夫曼树
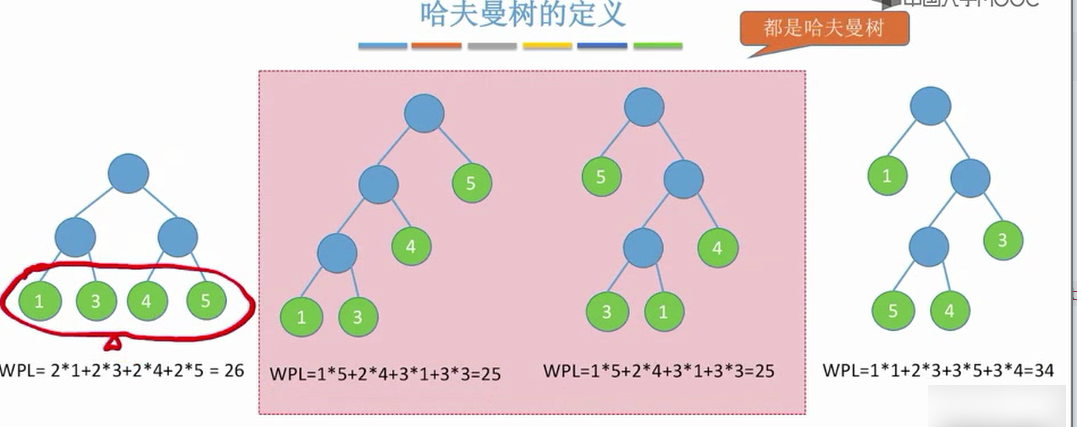
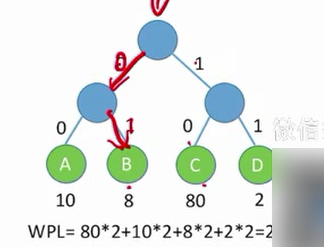
带权路径长度
结点的权:有某种现实含义的数值(如:表示节点的重要性等)
结点的带权路径长度:从树的根到该结点的路径长度(经过的边数)与该节点上权值的乘积。
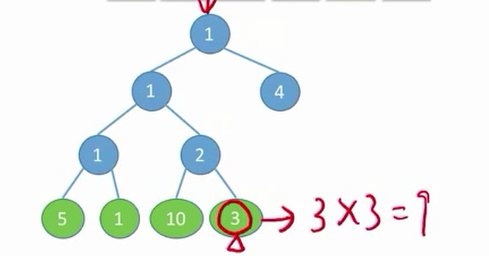
树的带权路径长度:树中所有叶节点的带权路径长度之和(WPL,Weighted Path Length)
[WPL=sum_{i=1}^nw_il_i
]
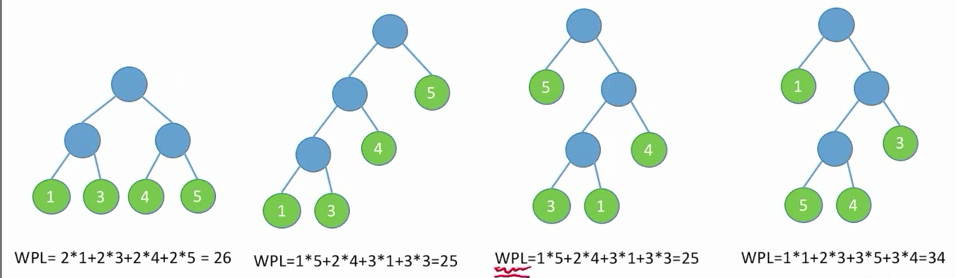
哈夫曼树:(最优二叉树) 在含有n个带权叶节点的二叉树中,其中带权路径长度(WPL)最小的二叉树称为哈夫曼树,也称最优二叉树。
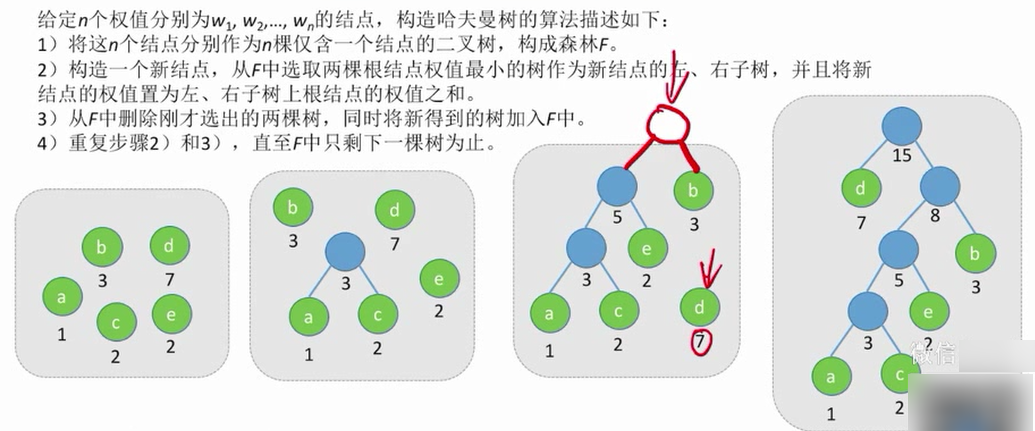
哈夫曼树的构造
每次先选择集合当中最小的两个,让它们成为兄弟。
两个树结合权值之和做为新根节点的权值。
n个结点,总共需要合并n-1次
每次合并都会增加多一个结点
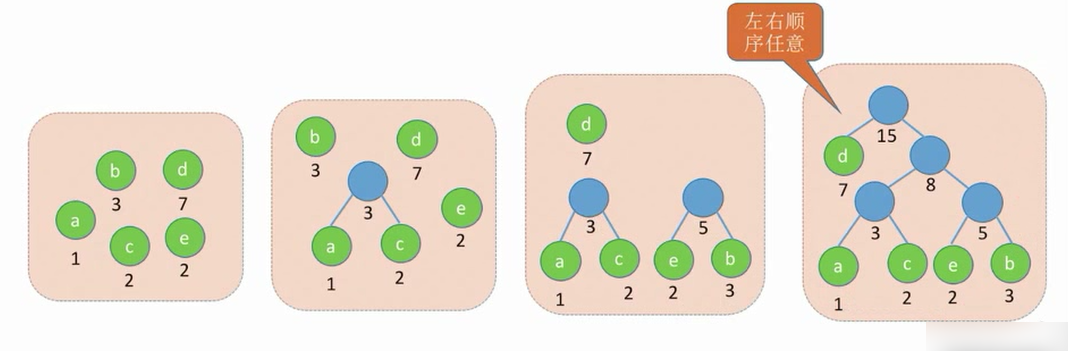
[WPL_{min}=1*7+2*3+3*2+4*1+4*2=31
]
- 每个初始结点最终都会成为叶节点,且权值越小的结点到根节点的路径长度越大。
- 哈弗曼树的结点总数为2n-1
- 哈夫曼树中不存在度为1的结点
- 哈夫曼树并不唯一,但WPL必然相同且为最优
哈夫曼编码
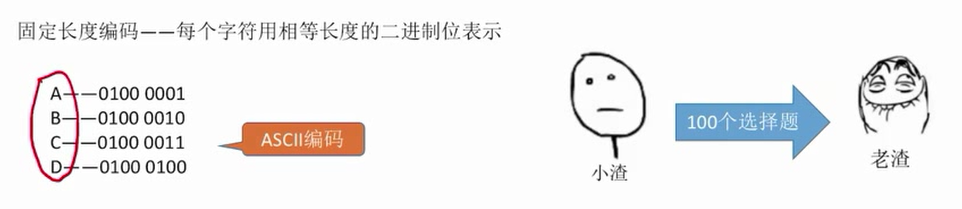

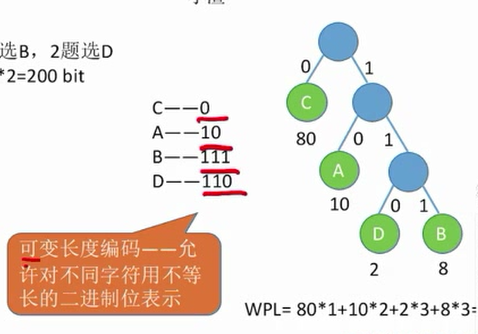
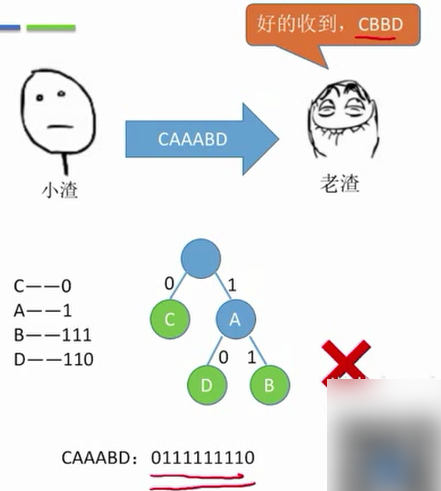
前缀编码:没有一个编码是另一个编码的前缀
哈夫曼编码可以用于数据的压缩