线索二叉树(找前驱/后继)
建立线索的初衷就是为了在一个结点中能够更方便找到前驱结点和后继结点。
- 中序线索二叉树
- 先序线索二叉树
- 后序线索二叉树
中序线索二叉树找中序后继
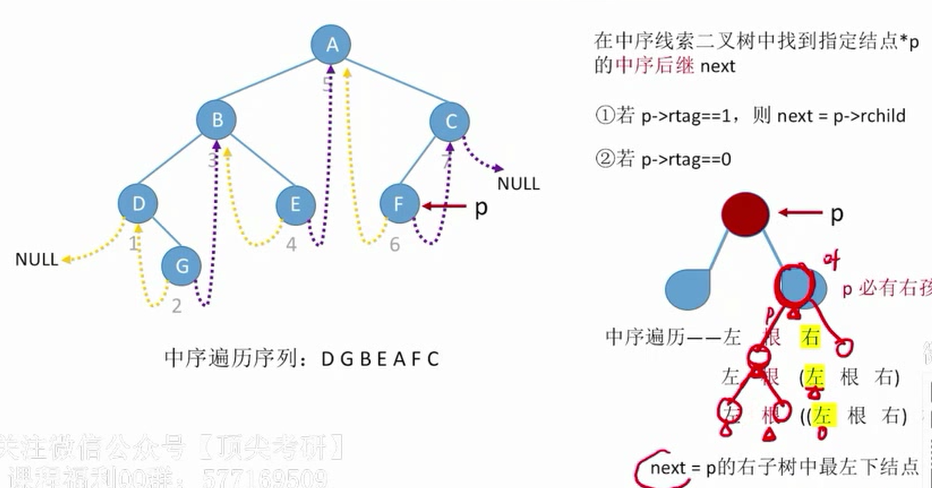
//找到以p为跟的子树中,第一个被中序遍历的结点
ThreadNode *Firstnode(ThreadNode *p){
//循环找到最左下角结点(不一定是叶子结点)
while(p->ltag==0) p=p->lchild;
return p;
}
//在中序线索二叉树中找到结点p的后继结点
ThreadNode *Nextnode(ThreadNode *p){
//右子树中最左下结点
if(p->rtag==0) return Firstnode(p->rchild);
else return p->rchild; //rtag==1 直接返回后继线索
}
//对中序线索二叉树进行中序遍历,(利用线索实现的非递归算法)
void Inorder(ThreadNode *T){
for(ThreadNode *p=Firstnode(T);p!=NULL;p=Nextnode(p))
visit(p);
}
空间复杂度
[O(1)
]
中序线索二叉树找中序前驱

在中序线索二叉树中找到指定结点*p的中序前驱pre
- 若p->ltag==1(被线索化了),则 pre=p->lchild(直接就是前驱)
- 若p->ltag==0(没有被线索化), 必定是有左孩子的。

//找到以p为根的子树中,最后一个被中序遍历的结点
ThreadNode *Lastnode(ThreadNode *p){
//循环找到最右下的结点(不一定是叶子结点)
while(p->rtag == 0) p=p-rchild;
return p;
}
//在中序线索二叉树中找到结点p的前驱结点
ThreadNode *Prenode(ThreadNode *p){
//左子树中最右下的结点
if(p->ltag=0) return Lastnode(p->lchild);
else return p->lchild;//ltag==1 直接返回前驱线索
}
//对中序线索二叉树进行逆向中序遍历
void RevInorder(ThreadNode *p){
for(ThreadNode *p=Lastnode(T);p!=NULL;p=Prenode(p))
visit(p);
}
先序线索二叉树找先序后继
在先序线索二叉树中找到指定结点*p的先序后继next
- 若p->rtag==1(被线索化了),则 next=p->rchild(直接就是前驱)
- 若p->rtag==0(没有被线索化), 必定是有右孩子的。

ThreadNode *find(ThreadNode *p){
if(p->lchild != NULL){
return p->lchild;
}else if(p->rchlid == NULL){
return p->rchild;
}else{
return null;
}
}
先序线索二叉树找先序前驱
在先序线索二叉树中找到指定结点*p的先序前驱pre
- 若p->ltag==1(被线索化了),则 pre=p->lchild(直接就是前驱)
- 若p->ltag==0(没有被线索化), 必定是有左孩子的。
先序遍历中,左右子树中的结点只可能是根节点的后继,不可能是前驱

- 如果能找到p的父节点,且p是左孩子
- 如果能找到p的父节点,且p是右孩子,其左兄弟为空
- 如果能找到p的父节点,且p是右孩子,其左兄弟非空
- 如果p是根节点,则p没有先序前驱
先一直往右边走,如果没得走了,在往左边走
后序线索二叉树找后序前驱
在后序线索二叉树中找到指定结点*p的后续前驱pre
- 若p->ltag==1,则pre=p->lchild
- 若p->ltag==0,必有左孩子

后序线索二叉树找后序后继

使用三叉链表来实现

