这是个数学解法,鄙人花了好久才想出来的,所以
求赞~~
臭不要脸
题面描述
求(1)~(n)区间各个数位上只有0与1的数字的个数。
思路讲解
打个表,分析一下
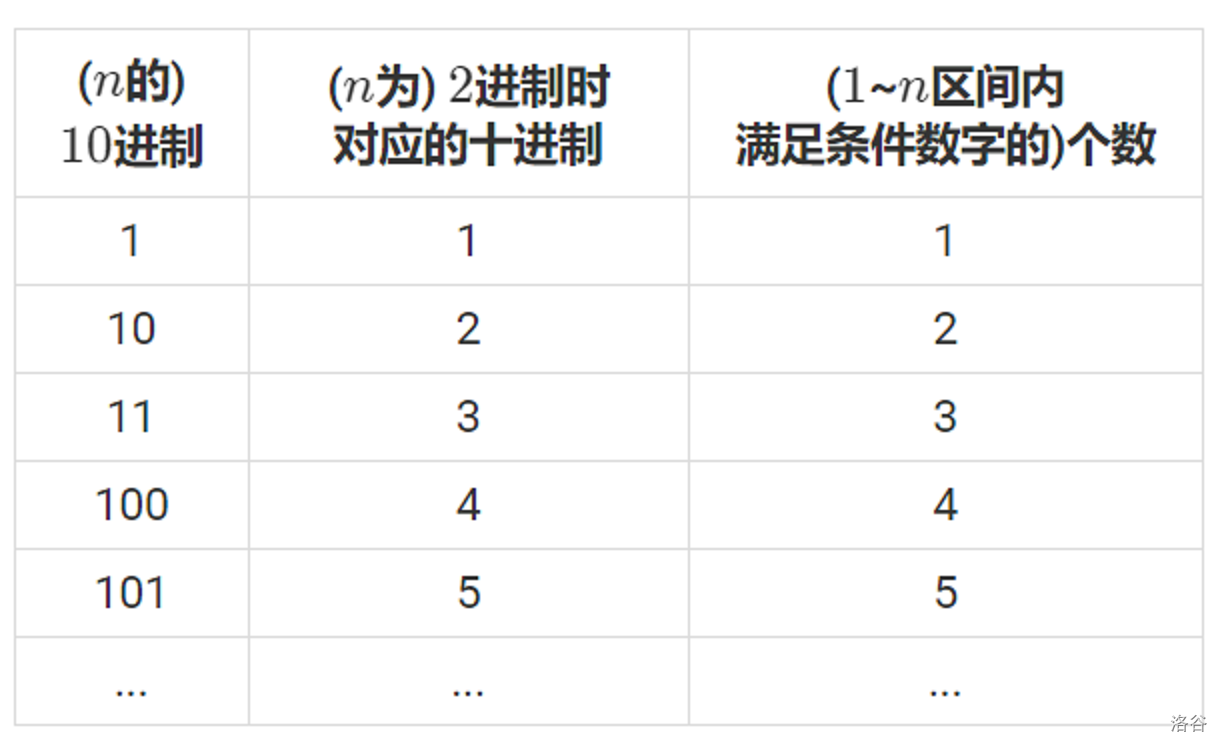
打表发现,在(n)恰好为像二进制的十进制时,个数对应的就是将(n)当作二进制看时所对应的十进制数的值
如果没那么巧,不是像二进制的十进制数时要如何处理呢?
我们很轻易的就能发现,在到达下一个像二进制的十进制数前,无论(n)多大,个数都是不变的。
举个栗子
(1)$11$区间内有$3$个**像二进制的十进制数**,$1$(12)区间内也有(3)个像二进制的十进制数,
(1)~(15)区间内也是一样的。
直到(n=100)时,数量才发生变化,变为了(4)个。
所以,得出结论:
(ans=) 将 最大的(≤n)的像二进制数的十进制数 看作二进制数时 所对应的十进制数值
是不是很绕
举个栗子
[n=13
]
最大的(≤n)的像二进制数的十进制数(=11)
将其看作二进制数时所对应的十进制数值(=3)
(ans=3) (数字分别有(1),(10),(11))
放一下找最大的(≤n)的像二进制数的十进制数的代码
bool flag=0;//用于标记上面几位是否有减小
int w[/*n的长度*/];//w数组用来存储n的各个数位
for(int i=0;i<len;i++)
{
if(flag)//如果上面几位有减小
w[i]++;//这一位必定是1
if(w[i]>1)//判断这位是否有减小
flag=1;
if(w[i])//只要不是0这位就必定是1
w[i]=1;
}
这一段思路不好了解,大家如有不懂建议多看几遍
剩下的数位分离和进制转换部分就不用我放代码了吧
祝大家新年快乐!!!
((write) (in) (2021/2/10),阴历腊月廿九)
留个赞再走吧( ̄︶ ̄)↗
(The) (End)