光照可分为局部光照和全局光照。
局部光照:直接照射到物体表面的光照
全局光照:物体表面受周围环境影响的光照
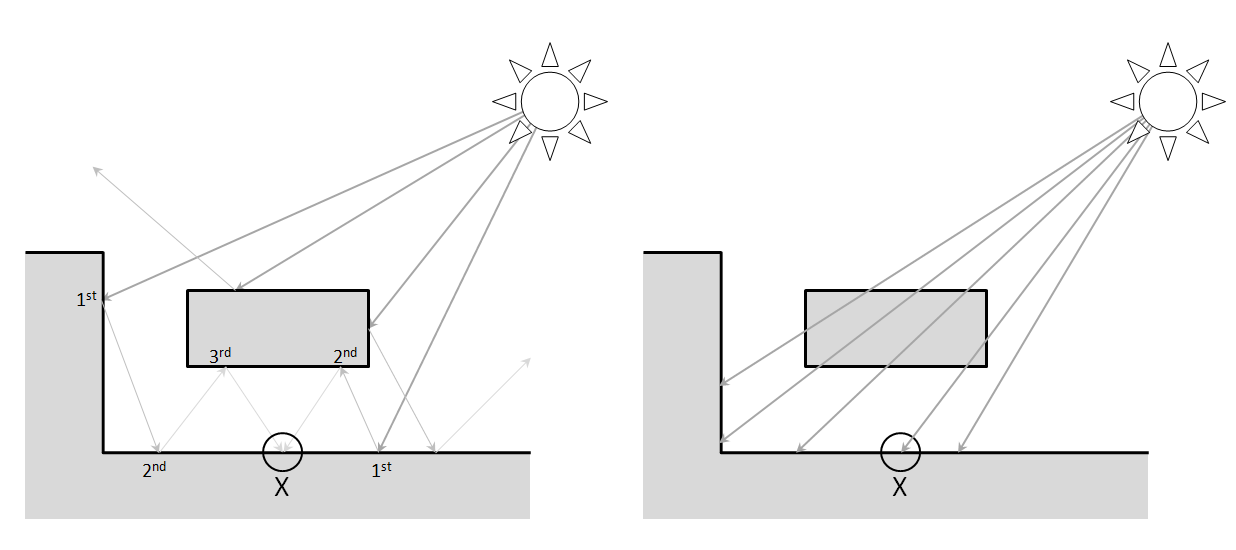
左图中点x接收到周围环境的光线照射,来自周围表面的反射光照称为全局光照;右图中点x接收来自太阳光的直接照射,来自太阳发射的直接光照称为局部光照。
在现实环境中,全局光照的情况更为复杂,例如:
- 半透明表面(Semi-transparent surfaces):光线可以穿过表面进行复杂的交互,如玻璃棱镜,可以改变光的波长;
- 次表面散射(Sub-Surface Scattering):光线可以穿过子表面,在同一表面的不同方向反射,如皮肤;
- 表面渗色(Surface bleeding):光线穿过表面,在介质中改变颜色到目标表面。
其他例子还有很多,全局光照会比局部光照效果更佳柔和自然,但考虑到其复杂性,应用到实时渲染中也是有一定难度的。
我们在前几篇中通过理论得到的BRDF光照模型公式实际为局部光照模型中,还欠缺了全局光照因素。
下面,我们来研究一下BRDF的局部反射模型,先来看下最简单的Lambertian反射模型。
Lambertian反射模型
Lambertian反射称作完全漫反射。这是一种理想情况,现实中不存在完全漫反射,但Lambertian可以用来近似的模拟一些粗糙表面的效果,比如纸张。
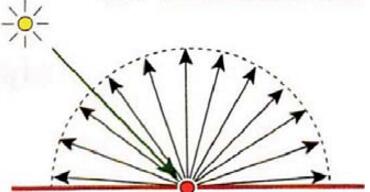
对于Lambertian表面,入射方向与出射方向无关,({omega_i})与({omega_o})无关,({L_o(p, omega_o)})可以表示为({L_o(p, omega_o)} = {L_r(p)})。
在上一篇中,我们知道反射辐射度的方程为:
({L_o(p,omega_o)} = int_{Omega_i}{f_r(p, omega_i, omega_o)}\, {L_i(p, omega_i)}\, {cos heta_i}\, {domega_i})
在Lambertian反射模型中,由于({omega_i})与({omega_o})无关,BRDF项({f_r(p, omega_i, omega_o)} = {f_r(p)}),上式可表示为:
({L_r(p)} = {f_r(p)int_{Omega_i}L_i(p, omega_i)\, cos heta_i \, domega_i} = {f_r(p)\, E_i(p)})
(Rightarrow {f_r(p)} = frac{L_r(p)}{E_i(p)})
在上一篇的反射率中,({Omega_o})内的反射通量({dPhi_o} = {dAint_{Omega_o}L_o(p,omega_o) \, cos heta_o \, domega_o})
在整个Lambertian表面半球积分(({Omega_o} = {2pi}))中:
({dPhi_o} = {dAL_r(p)int_{2pi}cos heta_o \, domega_o} = {dA \, L_r(p) \, pi})
式中的({int_{2pi}cos heta_o \, domega_o} = {pi}),这是一个半球积分,在第一篇中我们推出过该结果。
({dPhi_i} = {dAint_{2pi} L_i(p, omega_i) \, cos heta_i \, domega_i} = {dA \, E_i(p)})
反射率({ ho_d(p)} = frac{dphi_o}{dphi_i} = frac{L_r(p) \, pi}{E_i(p)} = {f_r(p) \, pi})
这样,我们就得到了Lambertain BRDF:({f_r(p)} = frac{ ho_d(p)}{pi})
其中({ ho_d})可以用常数项表示:({ ho_d} = {k_d \, c_d}),({k_d in [0, 1]}),表示漫反射系数;({c_d})表示漫反射颜色。
Lambertain BRDF又可写为({f_r(p)} = frac{k_d \, c_d}{pi})
我们通常在实时渲染出于性能方面的考虑,会省略掉(pi),我们熟知的漫反射颜色计算公式,就是从反射辐射度方程中简化而来的:
反射辐射度方程:({L_o(p,omega_o)} = {f_r(p, omega_i, omega_o)}int_{Omega_i}{L_i(p, omega_i)}\, {cos heta_i}\, {domega_i})
漫反射着色公式:({L_r} = {k_d \, c_d} {sum_{1}^{n} \, L_i \, (n * l)} )
对比看一下,是不是很像?(sum_{1}^{n})表示逐个光源求和近似积分,({L_i})表示光源强度,({n * l})表示({cos heta_i})项