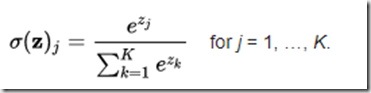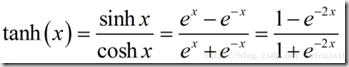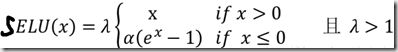TensorFlow神经网络中的激活函数

激活函数是人工神经网络的一个极其重要的特征。它决定一个神经元是否应该被激活，激活代表神经元接收的信息与给定的信息有关。

激活函数对输入信息进行非线性变换。 然后将变换后的输出信息作为输入信息传给下一层神经元。

激活函数的作用

当我们不用激活函数时，权重和偏差只会进行线性变换。线性方程很简单，但解决复杂问题的能力有限。没有激活函数的神经网络实质上只是一个线性回归模型。激活函数对输入进行非线性变换，使其能够学习和执行更复杂的任务。我们希望我们的神经网络能够处理复杂任务，如语言翻译和图像分类等。线性变换永远无法执行这样的任务。

激活函数使反向传播成为可能，因为激活函数的误差梯度可以用来调整权重和偏差。如果没有可微的非线性函数，这就不可能实现。

总之，激活函数的作用是能够给神经网络加入一些非线性因素，使得神经网络可以更好地解决较为复杂的问题。

在最新版本的TensorFlow 1.4.0（https://www.tensorflow.org/）中包含的激活函数：sigmoid，softmax，relu，elu，selu，softplus，softsign，tanh，hard_sigmoid，linear，serialize，deserialize等，具体介绍如下：

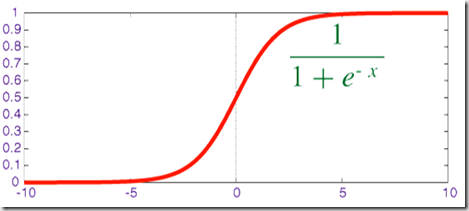
Sigmoid函数如下：作用是计算 x 的 sigmoid 函数。具体计算公式为 y=1/(1+exp(−x))，将值映射到[0.0 , 1.0]区间

    当输入值较大时,sigmoid将返回一个接近于1.0的值,而当输入值较小时,返回值将接近于0.0.

   优点：在于对在真实输出位于[0.0,1.0]的样本上训练的神经网络,sigmoid函数可将输出保持在[0.0,1.0]内的能力非常有用.

   缺点：在于当输出接近于饱和或者剧烈变化是,对输出返回的这种缩减会带来一些不利影响.

   当输入为0时,sigmoid函数的输出为0.5,即sigmoid函数值域的中间点

函数图像如下所示：

softmax函数：也是一种sigmoid函数，但它在处理分类问题时很方便。sigmoid函数只能处理两个类。当我们想要处理多个类时，该怎么办呢？只对单类进行“是”或“不是”的分类方式将不会有任何帮助。softmax函数将压缩每个类在0到1之间，并除以输出总和。它实际上可以表示某个类的输入概率。

比如，我们输入[1.2,0.9,0.75]，当应用softmax函数时，得到[0.42,0.31,0.27]。现在可以用这些值来表示每个类的概率。

softmax函数最好在分类器的输出层使用。

其定义为：

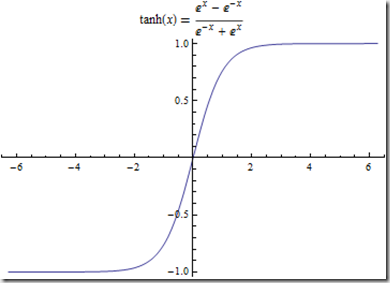
tanh函数如下：将值映射到[-1,1]区间

tanh与sigmoid非常接近,且与后者具有类似的优缺点, sigmoid和tanh的主要区别在于tanh的值为[-1.0,1.0]

优点在于在一些特定的网络架构中,能够输出负值的能力十分有用.

缺点在于注意tanh值域的中间点为0.0,当网络中的下一层期待输入为负值或者为0.0时,这将引发一系列问题.

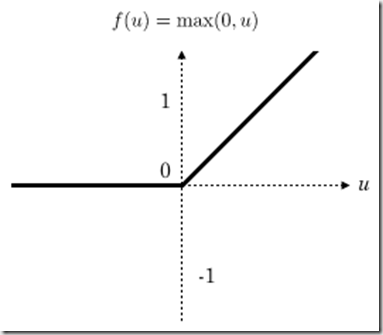
Relu（Rectified Linear Units修正线性单元）函数如下：relu函数是目前用的最多也是最受欢迎的激活函数。

relu在x<0时是硬饱和。由于当x>0时一阶导数为1。所以，relu函数在x>0时可以保持梯度不衰减，从而缓解梯度消失问题，还可以更快的去收敛。但是，随着训练的进行，部分输入会落到硬饱和区，导致对应的权重无法更新。我们称之为“神经元死亡”。

公式和函数图像如下

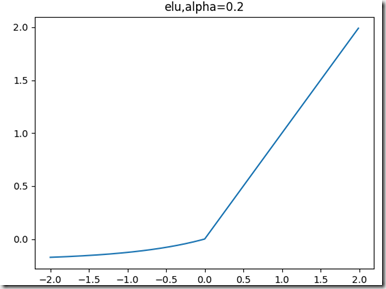
elu函数：是relu激活函数的改进版本，解决部分输入会落到硬饱和区，导致对应的权重无法更新的问题。计算激活函数relu，即max(features, 0)，所有负数都会归一化为0，所以的正值保留为原值不变

    优点：在于不受”梯度消失”的影响,且取值范围在[0,+oo)

    缺点：在于使用了较大的学习速率时,易受达到饱和的神经元的影响

公式和图像如下：左边缩小方差，右边保持方差；方差整体还是缩小的，而均值得不到保障。

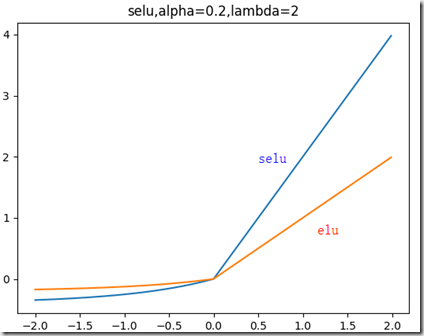
selu函数：

    左边缩小方差，右边放大方差，适当选取参数alpha和lambda，使得整体上保持方差与期望。如果选取：

    lambda=1.0506，alpha=1.67326，那么可以验证如果输入的x是服从标准正态分布，那么SELU(x)的期望为0，方差为1.

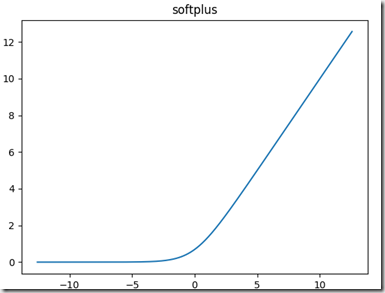
softplus函数:可以看作是relu函数的平滑版本，公式和函数图像如下：

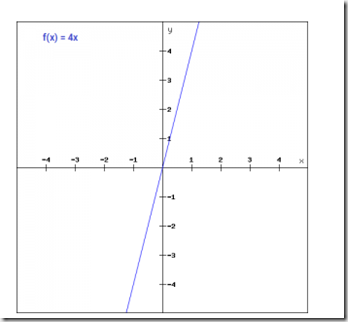
线性函数linear

   我们看到了step函数的问题，梯度为零，在反向传播过程中不可能更新权重和偏差。此时，我们可以用线性函数来代替简单的step函数。函数表达式：

f（x）=ax+b,

如何选择激活函数？

激活函数好或坏，不能凭感觉定论。然而，根据问题的性质，我们可以为神经网络更快更方便地收敛作出更好的选择。

用于分类器时，Sigmoid函数及其组合通常效果更好。

由于梯度消失问题，有时要避免使用sigmoid和tanh函数。

ReLU函数是一个通用的激活函数，目前在大多数情况下使用。

如果神经网络中出现死神经元，那么PReLU函数就是最好的选择。

请记住，ReLU函数只能在隐藏层中使用。

一点经验：你可以从ReLU函数开始，如果ReLU函数没有提供最优结果，再尝试其他激活函数。

梯度知识补充

在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。比如函数f(x,y), 分别对x,y求偏导数，求得的梯度向量就是(∂f/∂x, ∂f/∂y)^T,简称grad f(x,y)或者▽f(x,y)。对于在点(x₀,y₀)的具体梯度向量就是(∂f/∂x₀, ∂f/∂y₀)^T.或者▽f(x₀,y₀)，如果是3个参数的向量梯度，就是(∂f/∂x, ∂f/∂y，∂f/∂z)^T,以此类推。

    那么这个梯度向量求出来有什么意义呢？它的意义从几何意义上讲，就是函数变化增加最快的地方。具体来说，对于函数f(x,y),在点(x₀,y₀)，沿着梯度向量的方向就是(∂f/∂x₀, ∂f/∂y₀)^T的方向是f(x,y)增加最快的地方。或者说，沿着梯度向量的方向，更加容易找到函数的最大值。反过来说，沿着梯度向量相反的方向，也就是 -(∂f/∂x₀, ∂f/∂y₀)^T的方向，梯度减少最快，也就是更加容易找到函数的最小值。

　　　　

在机器学习算法中，在最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数，和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。

　　　　梯度下降法和梯度上升法是可以互相转化的。比如我们需要求解损失函数f(θ)的最小值，这时我们需要用梯度下降法来迭代求解。但是实际上，我们可以反过来求解损失函数 -f(θ)的最大值，这时梯度上升法就派上用场了。

关于更多梯度下降，梯度上升的信息，参考https://www.cnblogs.com/pinard/p/5970503.html