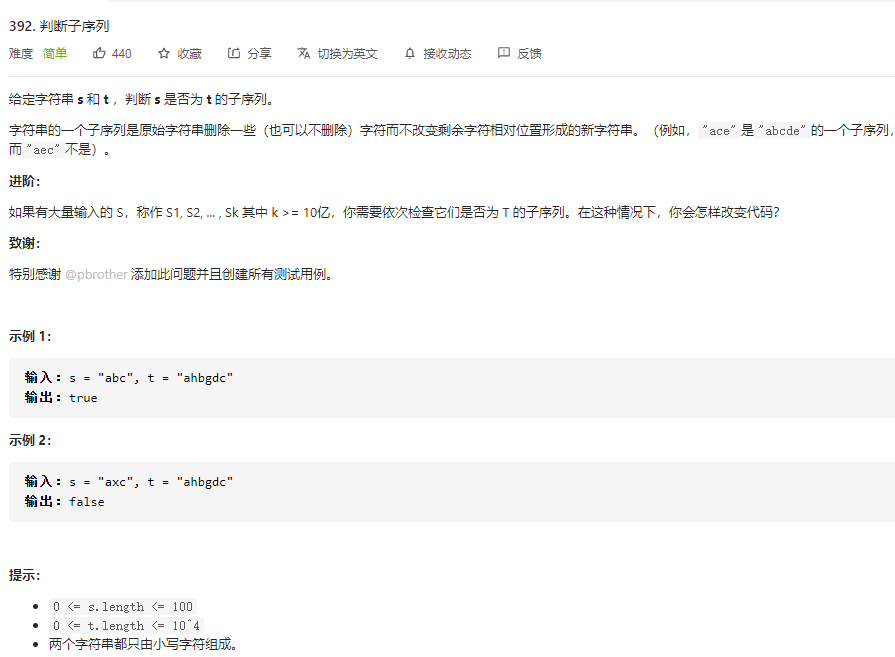
题目要求s需要是t的子序列,子序列的定义是t中删除一些元素能够与s保持一致。
类似的题目有求2个字符串的最长公共子序列,经典的DP题。
不过本题我们可以偷懒使用双指针来处理,可以把题目简化为
s中的每一个字符是否都能在t中找到对应
时间O(m+n)(m、n分别为字符串s和t的长度),空间O(1)
1 public boolean isSubsequence(String s, String t) { 2 int i=0,j=0; 3 while(i<s.length() && j<t.length()){ 4 if(s.charAt(i)==t.charAt(j)){ 5 i++; 6 } 7 j++; 8 } 9 return i==s.length(); 10 }
对于进阶问题,当我们在遇到超多字符串需要匹配时,如果我们
还使用上面方案的话,实际比较时间将会线性上升到k*(m+n)
于是我们可以参照KMP的next数组对字符串t做处理,
由于题目限定了s和t都只包含了小写字母,我们可以初始化一个
数组,存储第i个位置后出现字符j的位置,即,当我们遍历字符串
t到第i位时,此时s对应的字符是j,需要将t中i推进至哪一位。
这样做的好处是可以避免了s与t中字符不匹配,t中下标需要逐个递推
造成的时间浪费。
对于dp[i][j],我们发现只存在2种可能,(1)第i位便是j(2)第i位不是j
对于情况1,我们有dp[i][j]=i,对于情况2,我们便需要向后查找,于是有do[i][j]=dp[i+1][j]
由于第2种情况的存在,建立dp数组时我们需要从后向前递推
时间O(m*26+n*k)(建立dp数组耗时m*26,逐个匹配字符串s耗时k*s),空间O(m*26)
1 public boolean isSubsequence(String s, String t) { 2 int n=s.length(),m=t.length(); 3 int[][] dp=new int[m+1][26]; 4 5 // 初始化边界值,dp[i][j] = m表示t中不存在字符j 6 for(int i=0;i<26;i++){ 7 dp[m][i] = m; 8 } 9 10 for(int i=m-1;i>=0;i--){ 11 for(int j=0;j<26;j++){ 12 // 从后向前递推,存在2种情况,t中第i个位置是j,那么 13 // dp[i][j]=i,否则就要向后查找,于是有dp[i][j]=dp[i+1][j] 14 if(t.charAt(i)==j+'a'){ 15 dp[i][j]=i; 16 }else{ 17 dp[i][j]=dp[i+1][j]; 18 } 19 } 20 } 21 22 int index=0; 23 for(int i=0;i<n;i++){ 24 // 表示在t的剩余空间内没有再出现s中的字符,直接返回 25 if(dp[index][s.charAt(i)-'a']==m){ 26 return false; 27 } 28 // 成功匹配,则继续往后查找 29 index=dp[index][s.charAt(i)-'a']+1; 30 } 31 32 return true; 33 }