树(tree)
- 定义
树是一种数据结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做 “树” 是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。树结构是一种非线性存储结构,存储的是具有“一对多”关系的数据元素的集合
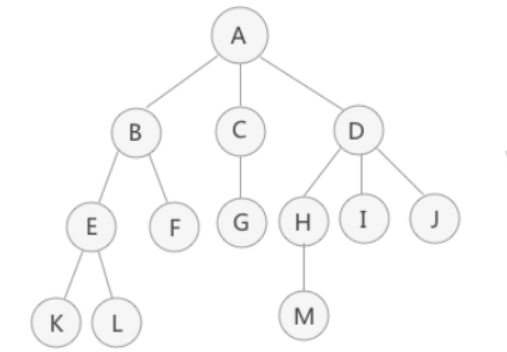
- 树的特点
每个节点有零个或多个子节点;
没有父节点的节点称为根节点;
每一个非根节点有且只有一个父节点;
除了根节点外,每个子节点可以分为多个不相交的子树;
- 二叉树
二叉树是树类结构中最常见的,也是运用最广泛的,二叉树是一种比较有用的折中方案,它添加,删除元素都很快,并且在查找方面也有很多的算法优化,所以,二叉树既有链表的好处,也有数组的好处,是两者的优化方案,在处理大批量的动态数据方面非常有用。它具有以下几个特点:
每个结点最多有两颗子树,结点的度最大为2。
左子树和右子树是有顺序的,次序不能颠倒。
即使某结点只有一个子树,也要区分左右子树。
二叉树中,第 i 层最多有 2i-1 个结点。
如果二叉树的深度为 K,那么此二叉树最多有 2K-1 个结点。
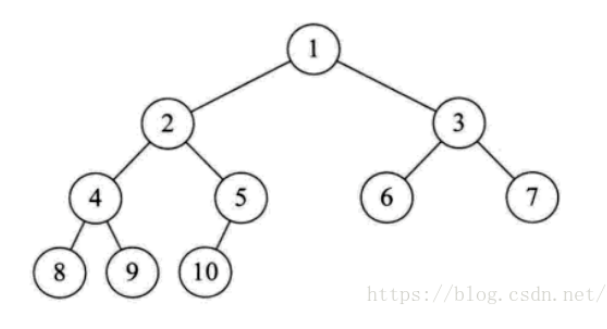
- 满二叉树和完全二叉树
满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
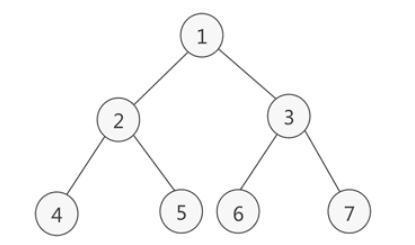
满二叉树具有以下性质:
满二叉树中第 n 层的节点数为 2n-1 个。
深度为 k 的满二叉树必有 2k-1 个节点 ,叶子数为 2k-1。
满二叉树中不存在度为 1 的节点,每一个分支点中都两棵深度相同的子树,且叶子节点都在最底层。
具有 n 个节点的满二叉树的深度为 log2(n+1)。
完全二叉树:如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树。
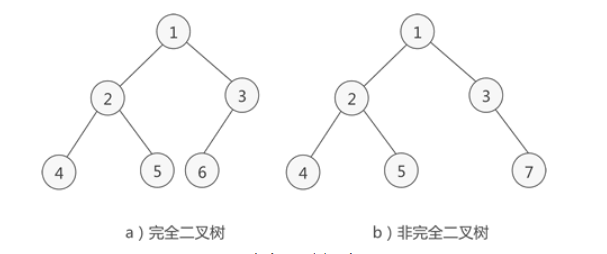
完全二叉树的性质:
满二叉树中第 n 层的节点数为 2n-1 个。
深度为 k 的满二叉树必有 2k-1 个节点 ,叶子数为 2k-1
n 个结点的完全二叉树的深度为 ⌊log2n⌋+1。
- 二叉树的遍历
先序遍历:
访问根节点;
访问当前节点的左子树;
若当前节点无左子树,则访问当前节点的右子树;

先序遍历具体过程:
- 访问该二叉树的根节点,找到 1;
- 访问节点 1 的左子树,找到节点 2;
- 访问节点 2 的左子树,找到节点 4;
- 由于访问节点 4 左子树失败,且也没有右子树,因此以节点 4 为根节点的子树遍历完成。但节点 2 还没有遍历其右子树,因此现在开始遍历,即访问节点 5;
- 由于节点 5 无左右子树,因此节点 5 遍历完成,并且由此以节点 2 为根节点的子树也遍历完成。现在回到节点 1 ,并开始遍历该节点的右子树,即访问节点 3;
- 访问节点 3 左子树,找到节点 6;
- 由于节点 6 无左右子树,因此节点 6 遍历完成,回到节点 3 并遍历其右子树,找到节点 7;
- 节点 7 无左右子树,因此以节点 3 为根节点的子树遍历完成,同时回归节点 1。由于节点 1 的左右子树全部遍历完成,因此整个二叉树遍历完成;
先序遍历的最终结果为:1,2,4,5,3,6,7
中序遍历:
访问当前节点的左子树;
访问根节点;
访问当前节点的右子树

中序遍历具体过程:
- 访问该二叉树的根节点,找到 1;
- 遍历节点 1 的左子树,找到节点 2;
- 遍历节点 2 的左子树,找到节点 4;
- 由于节点 4 无左孩子,因此找到节点 4,并遍历节点 4 的右子树;
- 由于节点 4 无右子树,因此节点 2 的左子树遍历完成,访问节点 2;
- 遍历节点 2 的右子树,找到节点 5;
- 由于节点 5 无左子树,因此访问节点 5 ,又因为节点 5 没有右子树,因此节点 1 的左子树遍历完成,访问节点 1 ,并遍历节点 1 的右子树,找到节点 3;
- 遍历节点 3 的左子树,找到节点 6;
- 由于节点 6 无左子树,因此访问节点 6,又因为该节点无右子树,因此节点 3 的左子树遍历完成,开始访问节点 3 ,并遍历节点 3 的右子树,找到节点 7;
- 由于节点 7 无左子树,因此访问节点 7,又因为该节点无右子树,因此节点 1 的右子树遍历完成,即整棵树遍历完成;
中序遍历的最终结果为:4,2,5,1,6,3,7
后序遍历:
从根节点出发
依次遍历各节点的左右子树,
直到当前节点左右子树遍历完成后,才访问该节点元素。

后序遍历具体过程:
- 从根节点 1 开始,遍历该节点的左子树(以节点 2 为根节点);
- 遍历节点 2 的左子树(以节点 4 为根节点);
- 由于节点 4 既没有左子树,也没有右子树,此时访问该节点中的元素 4,并回退到节点 2 ,遍历节点 2 的右子树(以 5 为根节点);
- 由于节点 5 无左右子树,因此可以访问节点 5 ,并且此时节点 2 的左右子树也遍历完成,因此也可以访问节点 2;
- 此时回退到节点 1 ,开始遍历节点 1 的右子树(以节点 3 为根节点);
- 遍历节点 3 的左子树(以节点 6 为根节点);
- 由于节点 6 无左右子树,因此访问节点 6,并回退到节点 3,开始遍历节点 3 的右子树(以节点 7 为根节点);
- 由于节点 7 无左右子树,因此访问节点 7,并且节点 3 的左右子树也遍历完成,可以访问节点 3;节点 1 的左右子树也遍历完成,可以访问节点 1;
- 到此,整棵树的遍历结束。
后序遍历最终结果:4,5,2,6,7,3,1
层次遍历:
通过使用队列的数据结构,从树的根结点开始,依次将其左孩子和右孩子入队。而后每次队列中一个结点出队,都将其左孩子和右孩子入队,直到树中所有结点都出队,出队结点的先后顺序就是层次遍历的最终结果。
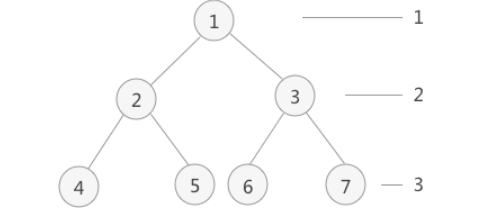
层次遍历具体过程:
- 首先,根结点 1 入队;
- 根结点 1 出队,出队的同时,将左孩子 2 和右孩子 3 分别入队;
- 队头结点 2 出队,出队的同时,将结点 2 的左孩子 4 和右孩子 5 依次入队;
- 队头结点 3 出队,出队的同时,将结点 3 的左孩子 6 和右孩子 7 依次入队;
- 不断地循环,直至队列内为空。
层次遍历最终结果:1,2,3,4,5,6,7