最近做题目饱受打击,愈发觉得打好基础的重要性,于是乎,决心把基本的排序算法还有数组操作一一实现,目的在于
一方面能够得到对JAVA基础的巩固,另一面在实现的过程中发现不足。
今天所实现的堆排序(最大堆)算法,最小堆大同小异。然后基于最大堆实现最大优先队列,最大优先队列可应用于作
业调度,比如可将作业长度作为关键字值,实现最长作业优先;或者将作业优先权值作为关键字值,实现高优先权作业优先
执行等等。
最大堆排序算法结构如下图:
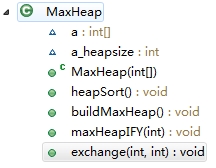

1 //:ThinkingInJava/com.mindview.fundamental/MaxHeap.java 2 package com.mindview.fundamental; 3 /** 4 * 5 * @Time 2014-6-17 6 * @Descri MaxHeap.java 最大堆排序实现算法 7 * parent (i-1)/2 8 * left 2*i+1 9 * right 2*i+2 10 * @author pattywgm 11 * 12 */ 13 public class MaxHeap { 14 int a[]; 15 int a_heapsize; 16 //接受数组 17 public MaxHeap(int a[]) { 18 this.a=a; 19 a_heapsize=a.length; 20 } 21 22 //堆排序 23 public void heapSort(){ 24 buildMaxHeap(); 25 for(int i=a.length-1;i>0;i--){ 26 //从大到小输出,实际数组顺序输出为从小到大 27 // System.out.print(a[0]+" "); 28 exchange(0, i); 29 a_heapsize=a_heapsize-1; 30 maxHeapIFY(0);//from top to bottom 31 } 32 } 33 34 //创建堆 35 public void buildMaxHeap(){ 36 //a[(a.length-1)/2] to a[0] is not leaf 37 for(int i=(a.length/2-1);i>=0;i--){ 38 maxHeapIFY(i); 39 } 40 } 41 //调整堆,以使其符合最大堆性质 42 public void maxHeapIFY( int i) { 43 int aLeft=2*i+1;//leftChild 44 int aRight=2*i+2;//rightChild 45 int largest; 46 if(aLeft<a_heapsize && a[aLeft]>a[i]) 47 largest=aLeft; 48 else 49 largest=i; 50 if(aRight<a_heapsize && a[aRight]>a[largest]) 51 largest=aRight; 52 if(largest!=i){ 53 exchange(i,largest); 54 //子树可能违反最大堆性质,继续调整 55 maxHeapIFY(largest); 56 } 57 58 59 } 60 //exchange A[i] with A[largest] 61 public void exchange(int i, int largest) { 62 int temp=a[i]; 63 a[i]=a[largest]; 64 a[largest]=temp; 65 66 } 67 } 68 69 ///:~
其中buildMaxHeap()实现建立最大堆,HeapSort()方法首先调用该方法建立最大堆,然后获取堆顶元素即为最大元素,
将其与堆底最后一个元素交换后输出到数组中,此时得到新的堆大小,并通过maxHeapIFY()方法继续调整堆,以使堆能够
满足最大堆性质。循环迭代该过程,即可实现最大堆的排序,数组中最后保存的元素顺序是从小到大的。
最大优先队列算法结构图如下:


1 //:ThinkingInJava/com.mindview.fundamental/MaxPriorityQueue.java 2 package com.mindview.fundamental; 3 /** 4 * 5 * @Time 2014-6-17 6 * @Descri MaxPriorityQueue.java 7 * 基于最大堆,实现最大优先队列,最大优先队列应用于作业调度 8 * 可将作业长度作为关键字,进行比较 9 * @author pattywgm 10 * 11 */ 12 public class MaxPriorityQueue { 13 int task[]; 14 MaxHeap heap; 15 public MaxPriorityQueue(int[] task) { 16 this.task=task; 17 heap=new MaxHeap(task); 18 heap.buildMaxHeap();//创建最大堆 19 } 20 //获取最大关键字 21 public int heapMaxiMum(){ 22 return task[0]; 23 } 24 //去掉并返回最大关键字 25 public int heapExtractMax(){ 26 if(heap.a_heapsize<1){ 27 System.out.println("Error:heap underflow"); 28 return -1; 29 } 30 else{ 31 int max=task[0]; 32 task[0]=task[heap.a_heapsize-1]; 33 heap.a_heapsize=heap.a_heapsize-1; 34 heap.maxHeapIFY(0); 35 return max; 36 } 37 } 38 //在堆中插入元素x 39 public void heapInsert(int x){ 40 task[heap.a_heapsize]=-1; 41 System.out.println("insert: "+heap.a_heapsize); 42 heap.a_heapsize=heap.a_heapsize+1; 43 if(heap.a_heapsize>task.length){ 44 System.out.println("Error:array overflow"); 45 return; 46 } 47 else{ 48 heapIncreaseKey(heap.a_heapsize-1,x); 49 } 50 } 51 //将元素x值增加到key 52 public void heapIncreaseKey(int i,int key){ 53 if(task[i]>=key){ 54 System.out.println("new key is not bigger than current key"); 55 return; 56 } 57 else{ 58 task[i]=key; 59 //parent: (i-1)/2 60 while(i>0 && task[(i-1)/2]<task[i]){ 61 heap.exchange(i, (i-1)/2); 62 i=(i-1)/2; 63 } 64 } 65 } 66 67 public void print(){ 68 for(int i=0;i<heap.a_heapsize;i++){ 69 System.out.print(task[i]+" "); 70 } 71 } 72 73 } 74 75 ///:~
初始化调用MaxHeap类的buildMaxHeap()实现建立最大堆,即初始的最大优先队列。该最大优先队列支持以下操作:
1)heapMaxiMum():获取最大关键字值(依据最大堆性质,实际上只是获取堆顶元素)
2)heapExtractMax():去掉并返回最大关键字值,此时应注意重新调整堆(包括堆的大小和重新排列)
3)heapInsert(key):在现有队列中插入元素key,该操作与4)结合实现
4) heapIncreaseKey(i,key):将队列中指定位置处的值增加到key,注意值增加后堆性质的满足与否并做出相
应调整
映射到作业调度的问题,可将作业优先权值作为关键字值,1)或 2)操作获取当前作业队列中具有最高优先权的作业
进行调度, 2)操作更符合实际情况,在调度的同时更新队列;3)操作当有新的作业到来时将其插入优先权队列,并遵守
最大优先权最先执行的原则;4)操作在作业执行过程中,可能某个在优先权队列中的作业急需被调用,而其当前优先权却
不高,那么就需要提高其优先权,以使其能够被尽早调度。
