HOG构造函数
CV_WRAP HOGDescriptor() :winSize(64,128), blockSize(16,16), blockStride(8,8), cellSize(8,8),nbins(9), derivAperture(1), winSigma(-1), histogramNormType(HOGDescriptor::L2Hys),L2HysThreshold(0.2), gammaCorrection(true), nlevels(HOGDescriptor::DEFAULT_NLEVELS)
{}
CV_WRAP HOGDescriptor(Size_winSize, Size _blockSize, Size _blockStride, Size _cellSize, int _nbins, int_derivAperture=1, double _winSigma=-1, int _histogramNormType=HOGDescriptor::L2Hys,double _L2HysThreshold=0.2, bool _gammaCorrection=false, int_nlevels=HOGDescriptor::DEFAULT_NLEVELS) : winSize(_winSize),blockSize(_blockSize), blockStride(_blockStride), cellSize(_cellSize),nbins(_nbins), derivAperture(_derivAperture), winSigma(_winSigma),histogramNormType(_histogramNormType), L2HysThreshold(_L2HysThreshold),gammaCorrection(_gammaCorrection), nlevels(_nlevels)
{}
CV_WRAP HOGDescriptor(const String&filename)
{
load(filename);
}
HOGDescriptor(const HOGDescriptor& d)
{
d.copyTo(*this);
}
我们看到HOGDescriptor一共有4个构造函数,前三个有CV_WRAP前缀,表示它们是从DLL里导出的函数,即我们在程序当中可以调用的函数。
HOG基本概念
在构造函数中,有几个参数非常重要,分别为winSize(64,128), blockSize(16,16), blockStride(8,8), cellSize(8,8), nbins(9)。在此,用几个示意图来表示。
a) 窗口大小winSize
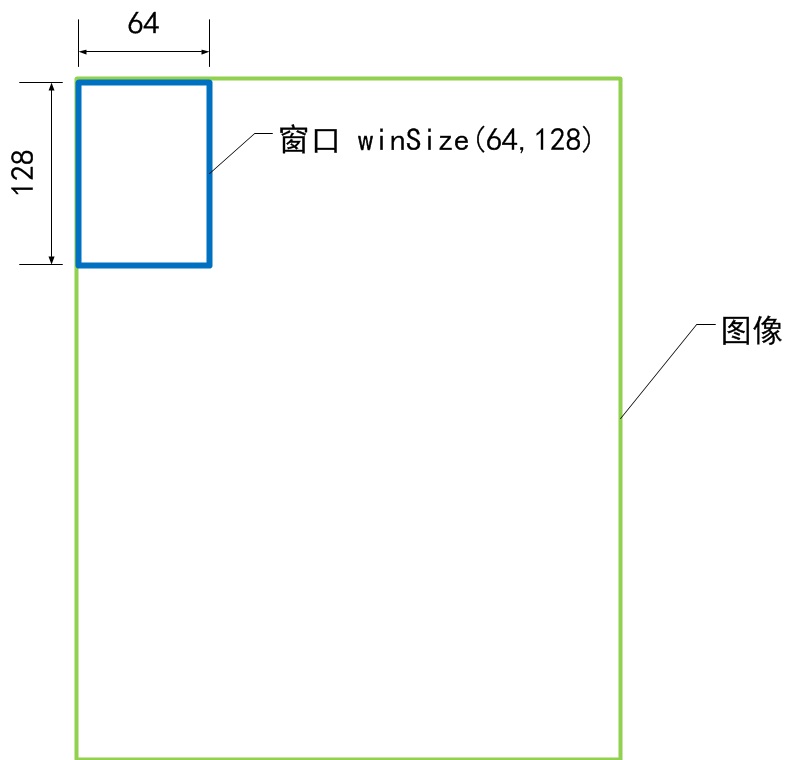
b) 块大小blockSize

c) 胞元大小cellSize
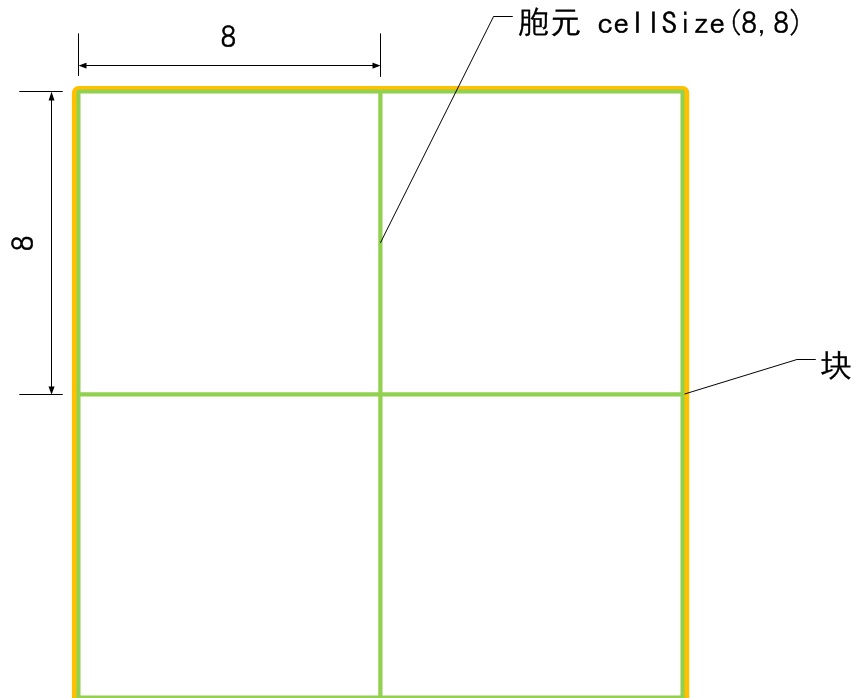
d) 梯度方向数
nbins代表在一个胞元中统计梯度的方向数目。如:nbins=9表示一个胞元内统计9个方向的梯度直方图。
Hog特征维数的计算
首先给出一个hog
HOGDescriptor* hog = newHOGDescriptor(cvSize(64, 48), cvSize(8, 6), cvSize(8, 6), cvSize(4, 3), 9);
根据上面的概念可知,cvSize(64,48)表示窗口的大小,cvSize(8, 6)表示块(block)大小,cvSize(8,6)表示块滑动增量(blockStride)大小,cvSize(4, 3)表示胞元(cell)大小,9表示每个胞单元中梯度直方图的数量。
注:输入的图片尺寸为640×480。
据此,可知:
一个块(block)包含A=(blockSize.width/cellSize.width)*(blockSize.height / cellSize.height)个胞元(cell),所以一个块(block)含有9A个梯度直方图。按照所给出的数据,可得结果为36。
一个窗口包含B=((windowSize.width-blockSize.width)/(blockStrideSize.width)+1)* ((windowSize.height-blockSize.height)/(blockStrideSize.height)+1)个块(block),所以一个窗口包含9AB个梯度直方图。
按照所给出的数据,可得结果为2304。
其次,计算特征向量hog->compute(trainImg,descriptors, Size(64, 48), Size(0, 0))
此处,trainImg代表输入的图片(此处尺寸为640×480),descriptors表示保存特征结果的Vector,Size(64,48)表示windows的步进,第四个为padding,用于填充图片以适应大小。
当padding以默认状态Size(0,0)出现,滑动窗口window来计算图片时,
结果不一定为整数。
此时,查看compute()函数发现,其中有一段代码如下:
padding.width = (int)alignSize(std::max(padding.width,0), cacheStride.width);
padding.height = (int)alignSize(std::max(padding.height,0), cacheStride.height);
这段代码就是用来将padding的大小来适应stride的大小。
在我的实例中,由于取得数都事先设计好,都是整数。而当若结果不为整数时,则将其取值为比其大的最小整数。如若padding.width计算为7.8时,就取8.
所以一幅640×480的图片,按照前面的参数,则可以取的特征数为230400维。
在此,特别感谢几位,分别为:
http://www.cnblogs.com/tornadomeet/archive/2012/08/15/2640754.html
此篇博文总结了一些网上的参考资料,采用Hog特征训练的流程及对OpenCV中Hog代码进行了解释
http://blog.csdn.net/raocong2010/article/details/6239431
此篇博文对Hog中Block,Cell的概念进行了详细的解释。我此篇博客中的图片来自于这篇博文。非常感谢。
http://gz-ricky.blogbus.com/logs/85326280.html
此篇博文对Hog中的特征个数计算进行了详细的解释