我们首先考虑一块石头高度变化对每个高度的查询的答案的影响,
即我们要记录,对于每个高度的查询的答案
所以要离散化高度(不然哪开的下数组啊)
不难发现,一次变化的对于不同高度的影响,对于一段连续高度是相同的
即一次修改操作,对于一段连续高度的答案,影响相同,满足区间修改性质
就决定是你了,树状数组
具体来说,考虑修改位置修改前后和两边的高度关系
但是情况很多,不妨把修改操作换成先删除(把高度降为0),再插入
考虑删除,插入的话,反过来就好,中间的是删除位置
情况1:中间比两边低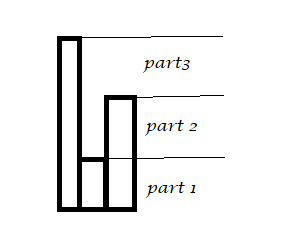
最简单的情况,不难发现,删除掉中间的只能让高度为$part1$的区间的答案$+1$,因为它割裂了两边的连续区间
情况2:中间比两边高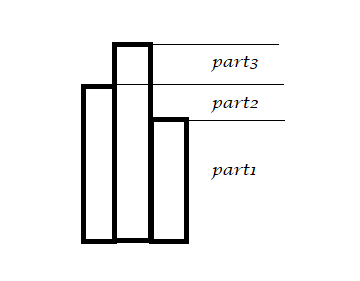
最高的区间影响就很广了
对于$part1:$它的删除会割裂两边的区间$val~of~part1++$
对于$part2:$因为两边没有构成连续区间,所以没有影响
对于$part3:$原来是有露出来的,现在没了,当然要减掉了
情况3:中间的高度也中等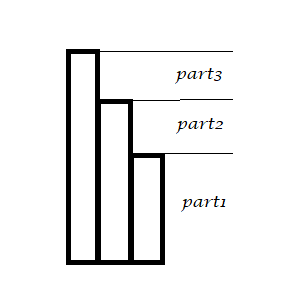
也很简单了,只对$part1$有影响
然而这样处理的只是答案的变化,我们还需要统计初始答案
还是考虑高度变化对答案的影响,不难发现,随着高度上升,未被覆盖的点的个数是单调不升的
按高度开$vector$,把每个高度恰好被覆盖的所有位置扔进去
从小到大枚举高度,先将这个高度的答案设为上一个高度的答案,取出这个高度恰好被覆盖的所有位置,统计这个位置的影响
如果它比两边高,类比上面情况2,答案减一
低呢,答案加一
这样我们就解决了这个问题
上代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
const int maxn=2e5+10;
vector<int>v[2*maxn];
int pre[2*maxn],n,m,a[maxn],mp[2*maxn],op[maxn],cnt,b[maxn],d[maxn],c[2*maxn];
bool vis[2*maxn];
int lowbit(int x)
{
return x&-x;
}
int sum(int x)
{
int ret=0;
while(x)
{
ret+=c[x];
x-=lowbit(x);
}
return ret;
}
void add(int x,int ch)
{
while(x<=cnt)
{
c[x]+=ch;
x+=lowbit(x);
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
mp[++cnt]=a[i];
}
for(int i=1;i<=m;i++)
{
scanf("%d",&op[i]);
if(op[i]==1)
scanf("%d",&b[i]),mp[++cnt]=b[i];
else
scanf("%d%d",&d[i],&b[i]),mp[++cnt]=b[i];
}
sort(mp+1,mp+cnt+1);
cnt=unique(mp+1,mp+cnt+1)-mp-1;
for(int i=1;i<=n;i++)
{
a[i]=lower_bound(mp+1,mp+cnt+1,a[i])-mp;
v[a[i]+1].push_back(i);
}
for(int i=1;i<=m;i++)
b[i]=lower_bound(mp+1,mp+cnt+1,b[i])-mp;
pre[1]=1,vis[0]=vis[n+1]=1;
for(int i=2;i<=cnt;i++)
{
pre[i]=pre[i-1];
for(int j=0;j<v[i].size();j++)
{
int u=v[i][j];
vis[u]=1;
if(!vis[u-1]&&!vis[u+1])
pre[i]++;
else if(vis[u-1]&&vis[u+1])
pre[i]--;
}
}
for(int i=1;i<=m;i++)
{
if(op[i]==1)
printf("%d
",pre[b[i]]+sum(b[i]));
else
{
int tmp[5];
tmp[1]=a[d[i]-1],tmp[2]=a[d[i]],tmp[3]=a[d[i]+1];
sort(tmp+1,tmp+4);
if(a[d[i]]>=a[d[i]-1]&&a[d[i]]>=a[d[i]+1])
add(tmp[2]+1,-1),add(tmp[3]+1,1);
add(1,1),add(tmp[1]+1,-1);
tmp[1]=a[d[i]-1],tmp[2]=b[i],tmp[3]=a[d[i]+1];
sort(tmp+1,tmp+4);
if(b[i]>=a[d[i]-1]&&b[i]>=a[d[i]+1])
add(tmp[2]+1,1),add(tmp[3]+1,-1);
add(1,-1),add(tmp[1]+1,1);
a[d[i]]=b[i];
}
}
return 0;
}