【机器学习速成宝典】模型篇02线性回归【LR】（Python版）

目录

　　什么是线性回归

　　最小二乘法

　　一元线性回归

　　多元线性回归

　　什么是规范化

　　Python代码(sklearn库)

---

什么是线性回归(Linear regression) 

　　引例

　　假设某地区租房价格只与房屋面积有关，我们现有数据集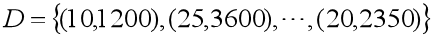，请用一条直线尽量去拟合所给的数据，从而达到预测房屋价格的效果。

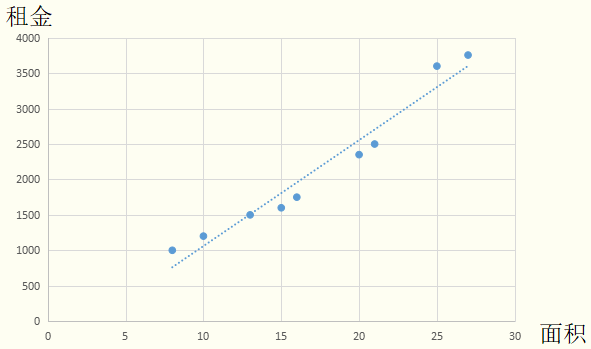
　　在引例中，面积是自变量，租金是因变量。使用直线去拟合训练集的数据，可得到面积-租金的函数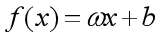：，即线性回归模型。利用此模型，输入面积后，便可预测出对应的租金。

　　百度百科定义

　　线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

最小二乘法(Least square method)

　　均方误差有很好的几何意义，它对应了常用的欧几里得距离，简称“欧氏距离”（Euclidean distance）。基于均方误差最小化来进行模型求解的方法称为“最小二乘法”。

　　结合引例中的数据解释最小二乘法的应用：

　　第一步：

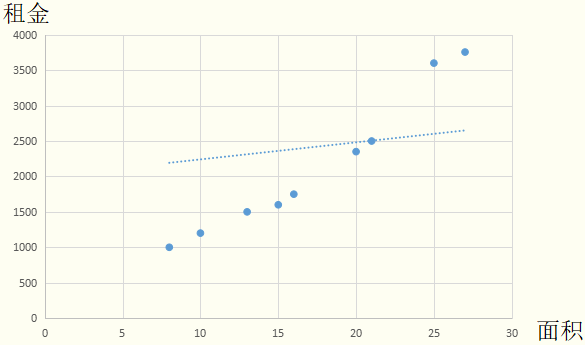
　　将训练集数据放入坐标平面。

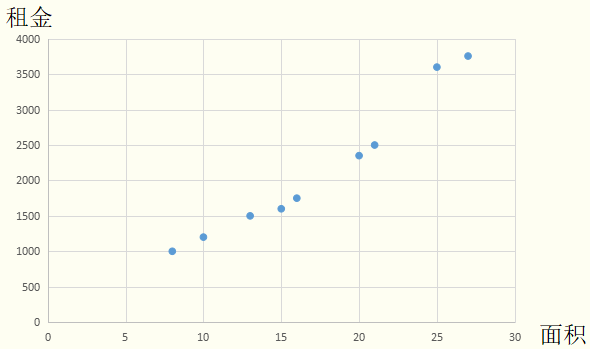
　　第二步：

　　假设一元线性回归模型为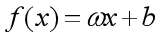，并绘制在坐标轴上。由于和是未知的，因此这里随意画一条。

　　第三步：

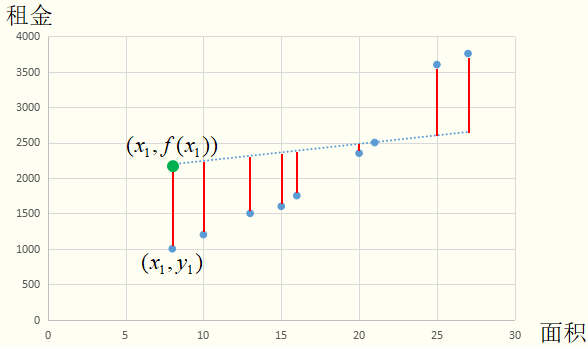
　　求每一个训练集中的数据到直线的欧氏距离。图中的红线长度并非点到直线的欧氏距离，做这种替代的优点是简化计算，又不影响最终求解结果。均方误差便可以用红线长度的累加表示。

　　第四步：

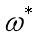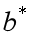　　让均方误差最小化，便可求出最优的和，即

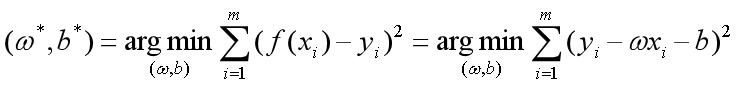
求解过程是使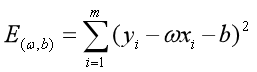（也称损失函数或代价函数）最小化的过程，称为线性回归模型的最小二乘“参数估计”（parameter estimation）。可以证明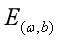是凸函数（有最小值）。我们可以将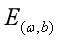分别对和求导，得到

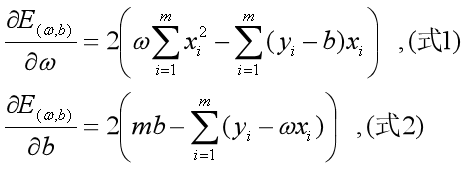
令（式1）和（式2）为0，联立求解二元一次方程组，可以得到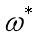和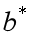最优解的闭式解：

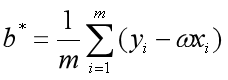
其中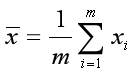为x的均值。

　　第五步：

　　将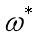和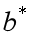代入假设一元线性回归模型，得到，即，这就是最终的一元线性回归模型。

至此，完成了最小二乘法的应用的讲解。

　　注意：“最小二乘法”不要与“梯度下降法”并列看待。“最小二乘法”是基于均方误差最小化来进行模型求解的方法，即用均方误差衡量模型的好坏程度，然后可以用“梯度下降法”让均方误差降到最低从而求解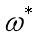和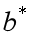，也可以像上文所述的求解析解的方法，即求导，令为0，解方程组，从而求解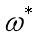和。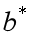

一元线性回归(Simple linear regression)

 　　引例其实就是典型的一元线性回归模型的求解问题，即只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示。由于一元线性回归模型只能考虑一个自变量的影响因素，看起来显得有点无力，不过之前所述是通向复杂模型的必经之路，其中的思想是相通的。只要能理解，想必在多元线性回归，乃至下一章的广义线性回归（logistic回归）的学习中也能游刃有余。

多元线性回归(Multivariate linear regression)

　　引例

　　假设某地区租房价格不仅与房屋面积有关，还与房间数、距离地铁站距离等等相关，比如有d种影响因素，那么训练数据集形式将由一元的

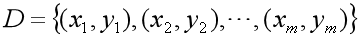
　　变为

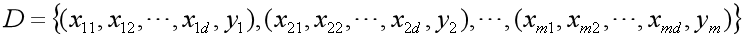
　　简记为

　　相应的将简记为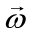，为了便于讨论，我们把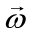和吸收入向量形式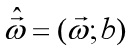，相应的，把数据集D表示为一个m×(d+1)大小的矩阵X，其中每一行对应于一个示例，该行前d个元素对应于示例的d个属性值，最后一个元素恒置为常数1，目的是：点乘的时候让常数1与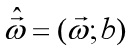中的相乘，从而保留一个待求解的截距项，即

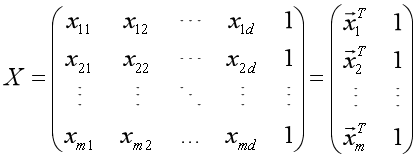
　　再把标记也写成向量形式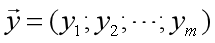。使用最小二乘法，通过均方误差最小化求解最优的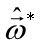，即

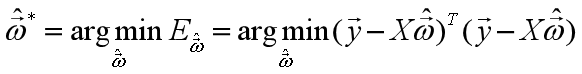
　　求解方法：

　　一、利用凸函数性质，可以使用梯度下降法（大数据下通常使用这个方法）求一个粗略的解。梯度下降法（Gradient descent）是求解无约束最优化问题的一种常用的方法，有实现简单的优点。梯度下降法是迭代算法，每一步需要求解目标函数的梯度向量，然后一步一步迭代运算，使得均方误差达到近似的最低。

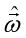　　二、利用凸函数性质，使用求解析解的方式，即求对的导数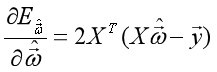，，令为0，求解方程组，可得到最优解的闭式解（求解中有一步求矩阵逆的运算，复杂度很高，大数据量时不推荐使用）

　　注意：当遇到的任务含有大量变量，其数目甚至超过样例数目时，导致X的列数多于行数，此时可以解出多个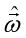，它们都能使均方误差最小化。常见的做法是引入正则化（Regularization）项。关于正则化的知识未来会在【黎明传数==>机器学习速成宝典】工程篇中讲到，敬请期待......

什么是规范化(Normalization) 

　　“规范化”是将不同变化范围的值映射到相同的固定范围中，常见的是[0,1]，此时也称“归一化”。

　　 好处是：

　　（1）在使用梯度下降法这种迭代最优化求解方法时，能提升模型的收敛速度，原理简单形容就是：没有规范化时，相当于要从一个椭圆边缘走到椭圆中心；规范化后，相当于从一个圆的边缘走向圆的中心。规范化会减少迭代计算的步数。

　　（2）提升模型的精度

Python代码(sklearn库)

# -*- coding: utf-8 -*-
from sklearn import linear_model
reg = linear_model.LinearRegression(fit_intercept=True,normalize=True,copy_X=True,n_jobs=-1)
'''
    @param fit_intercept: 是否需要计算截距值b
    @param normalize: 是否将训练样本归一化，归一化可以提升模型的收敛速度，提升模型精度
    @param copy_X: 真，X会被复制一份；假，X会被覆盖掉
    @param n_jobs: 任务并行时指定使用的CPU数，-1表示使用所有可用的CPU
    
    @attribute coef_: 权重向量
    @attribute intercept_: 截距b
    
    @method fit(X,y[,sample_weight]): 训练模型
    @method predict(X): 预测
    @method score(X,y[,sample_weight]): 计算在(X,y)上的预测的准确率
'''
#一元线性回归
trainX = [[10], [25], [20]]
trainY = [1200, 3600, 2350]
reg.fit (trainX, trainY)
print "权值："+str(reg.coef_)
print "截距："+str(reg.intercept_)

#多元线性回归
trainX = [[10,600], [25,800], [20,500]]
trainY = [1200, 3600, 2350]
reg.fit (trainX, trainY)
print "权值："+str(reg.coef_)
print "截距："+str(reg.intercept_)

'''运行结果
权值：[ 153.57142857]
截距：-432.142857143
权值：[ 134.28571429    1.92857143]
截距：-1300.0
'''