深度学习面试题02：标准梯度下降法

目录

　　一元函数的梯度下降法

　　多元函数的梯度下降法

　　参考资料

---

梯度下降是一种迭代式的最优化手段，在机器学习中一般用于求目标函数的极小值点，这个极小值点就是最优的模型内部参数。相比求解析解的手段，GD的通用性更强，所以受到广泛的使用。

一元函数的梯度下降法

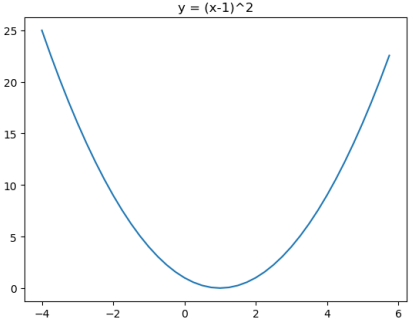
比如求解f(x)=(x-1)²的最小值点

梯度下降的公式为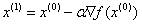，上标表示第i轮的x值

初始化点x⁽⁰⁾ = 4，学习率α= 0.25

第①次迭代：

x⁽¹⁾= 4 - 0.25*2(4-1)=2.5

 

第②次迭代：

x⁽²⁾= 2.5 - 0.25*2(2.5-1)=1.75

 

第③次迭代：

X⁽³⁾= 1.75 - 0.25*2(1.75-1)=1.375

 

上图中红色箭头表示梯度方向，每次迭代都朝着负梯度方向移动，可以看出，随着迭代次数的增加，x会趋近于x=1，使得y最小

 返回目录

多元函数的梯度下降法

比如求解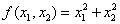的最小值点

梯度下降的公式为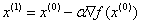，上标表示第i轮x的向量

 

 

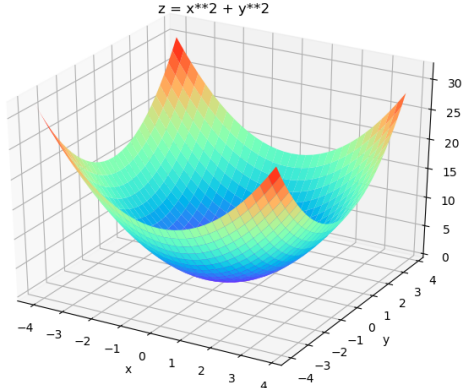
初始化点x⁽⁰⁾ = [-4;4]，学习率α= 0.25

第①次迭代：

x⁽¹⁾= [-4;4] - 0.25*2[-4;4]=[-2;-2]

 

第②次迭代：

x⁽²⁾= [-2;-2] - 0.25*2[-2;-2]=[-1;1]

 

第③次迭代：

x⁽²⁾= [-1;1] - 0.25*2[-1;1]=[-0.5;0.5]

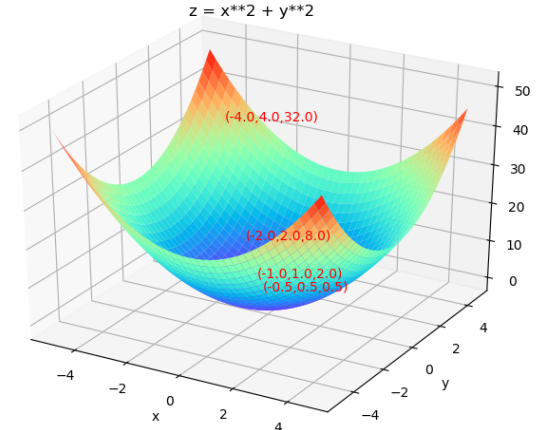
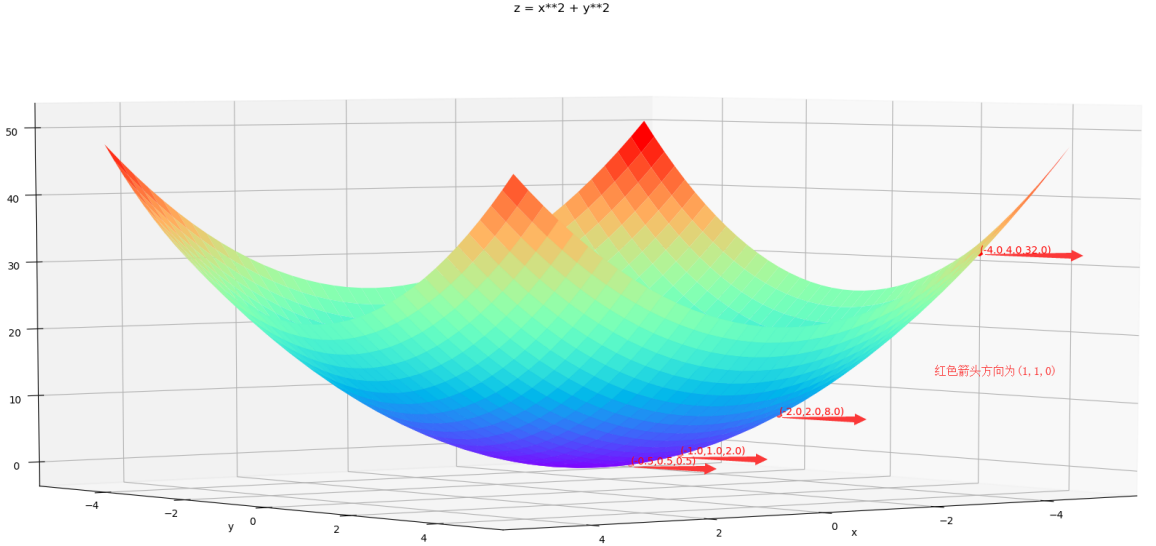
上图中红色箭头表示梯度方向，每次迭代都朝着负梯度方向移动，可以看出，随着迭代次数的增加，x会趋近于x=[0;0]，使得z最小

 返回目录

参考资料

 《图解深度学习与神经网络：从张量到TensorFlow实现》_张平

 返回目录