N叉树的最大深度-DFS

再看这道题之前，先来一道类似的简单题。

题目：求二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

3
/
9 20
/
15 7
返回它的最大深度 3 。

来源：leetcode
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

这道题思路很简单，因为是二叉树，有两个子节点，我们可以用递归依次求出左子树的深度和右子树的深度，然后两个进行比较，取最大的，得出的记过+1，因为还有根节点的那层。所以代码就好写了。

class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
    }
}

再来看这道题，这道题是上面那道题的变形，由二叉树变成了N叉树。

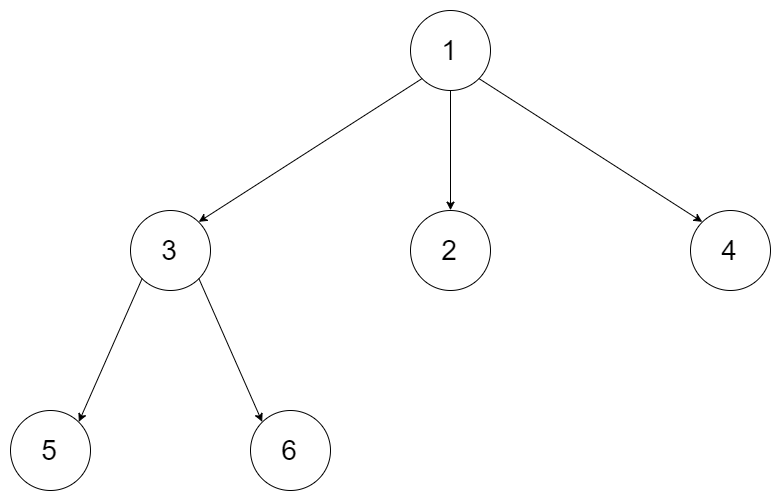
题目

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数
说明:
树的深度不会超过 1000。
树的节点总不会超过 5000。
看他给出的N叉树的定义。

class Node {
    public int val;
    public List<Node> children;//孩子节点是个集合

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};

要想求出N叉树的最大深度，就是求出N叉树的子节点中最大深度+1，那么求N叉树子节点有可变为求出当前节点的所有子节点中最大的深度。因此这道题可以通过DFS深度优先遍历来解决。

class Solution {
    public int maxDepth(Node root) {
        if(root==null){
            return 0;
        }
        if(root.children==null){
            return 1;
        }
        int res = 0;
        //遍历当前节点下面的所有子节点，求出子节点中最大深度
        for(int i=0;i<root.children.size();i++){
            res = Math.max(res,maxDepth(root.children.get(i)));
        }
        // 返回子节点中最大深度+1
        return res+1;
    }
}

唉，以后还得多刷刷有关树的题目。

“旅途“永无止境！