地址 https://pintia.cn/problem-sets/994805342720868352/problems/994805523835109376
题目的大意是
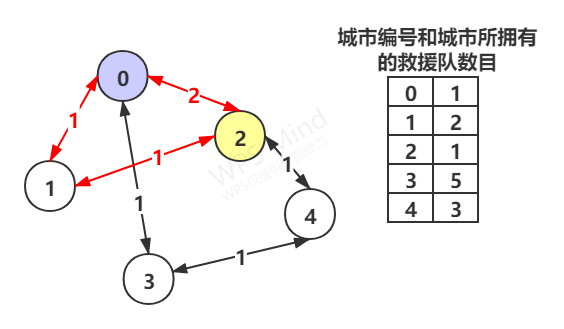
输入一群城市之间(0~n-1)的路径和该城市拥有的救援队数目,再给与你起点城市的编号和终点城市的编号, 请输出起点到终点城市的最短路径有几条,和最短路径上能收集的最大救援队的数目 输入格式 第一行4个数 n m s e. n表示城市的个数(0~n-1) , m表示城市之间的路径 , s表示起点城市的编号, e表示终点城市的编号 第二行 有n个数字 表示每个城市拥有的救援队数目 下面是m行 每行三个数字 a b l. a表示一个城市编号 b表示一个城市编号 l表示两城市之间的距离(道路是双向的) 输出格式 输出两个 数字 j k. j表示最短路径有多少条 k表示能收集的最大救援队数目 用空格隔开 示例 Sample Input: 5 6 0 2 1 2 1 5 3 0 1 1 0 2 2 0 3 1 1 2 1 2 4 1 3 4 1 Sample Output: 2 4
解答
考虑到数据范围不大 基本都在几百以内,可以直接DFS加上剪枝即可搞定
想进一步深入学习的同学可以考虑学习图论算法
使用DFS 尝试从0点出发 到终点2的各种走法,不断更新每个城市从0点出发能够达到的最短路径。
如果当前达到X点的走法的路径比之前到达X点的走法的路径要长,那么这种走法就不需要继续尝试了,因为按照这种走法达到后面的点肯定不是最短路径(剪枝)
if (currDis > dist[x]){return;}
如果当前达到X点的走法的路径比之前到达X点的走法的路径相等,
那么就需要记录达到该点的最短路径的个数,
path[x]++;
同时还需要更新下能收集到救援队数目
sum[x] = max(currSum,sum[x] );
#include <iostream> #include <vector> #include <algorithm> #include <memory.h> using namespace std; const int N = 700; const int INF = 0x3f3f3f3f; int graph[N][N]; int teams[N]; int start = -1; int endp = -1; int n, m; int path[N]; int dist[N]; int sum[N]; void dfs(int curr,int currDis, int currPath, int currSum) { //剪枝 当前走法走到curr点已经不可能更短了 if (currDis > dist[curr]){return;} if (currDis < dist[curr]) { dist[curr] = currDis; sum[curr] = currSum; path[curr] = 1; } else if (currDis == dist[curr] ) { sum[curr] = max(currSum,sum[curr] ); path[curr]++; } if (curr == endp) { return; } for (int i = 0; i < n; i++) { if (i != curr && graph[curr][i] != INF) { //currPath++; currSum += teams[i]; currDis += graph[curr][i]; dfs(i, currDis,currPath, currSum); //currPath--; currSum-= teams[i]; currDis -= graph[curr][i]; } } return; } int main() { //接受输入 得到 城市的个数和路径的个数 已经起点城市和终点城市 cin >> n >> m >> start >> endp; //得到输入的每个城市的救援队数目 for (int i = 0; i < n; i++) { cin >> teams[i]; } //初始化 图所有路径为最大值0x3f3f3f3f memset(graph,0x3f,sizeof(graph)); memset(dist, 0x3f, sizeof dist); //得到两个城市之间的路径 for (int i = 0; i < m; i++) { int a, b, l; cin >> a >> b >> l; graph[a][b] = min(graph[a][b],l); graph[b][a] = min(graph[b][a], l); } dfs(start,0,0, teams[start]); cout << path[endp] << " " << sum[endp] << endl; return 0; }

