地址 https://www.acwing.com/problem/content/885/
输入一个包含n个方程n个未知数的线性方程组。
方程组中的系数为实数。
求解这个方程组。
下图为一个包含m个方程n个未知数的线性方程组示例:
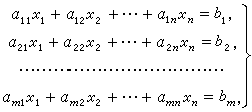
输入格式
第一行包含整数n。
接下来n行,每行包含n+1个实数,表示一个方程的n个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解,则输出共n行,其中第i行输出第i个未知数的解,结果保留两位小数。
如果给定线性方程组存在无数解,则输出“Infinite group solutions”。
如果给定线性方程组无解,则输出“No solution”。
数据范围
1≤n≤1001≤n≤100,
所有输入系数以及常数均保留两位小数,绝对值均不超过100。
输入样例: 3 1.00 2.00 -1.00 -6.00 2.00 1.00 -3.00 -9.00 -1.00 -1.00 2.00 7.00 输出样例: 1.00 -2.00 3.00
解法

使用多个方程变换系数 减少变量x 最终得到答案。
代码如下
#include <iostream> #include <vector> #include <vector> #include <math.h> using namespace std; const int N = 110; const double eps = 1e-6; int n; double a[N][N]; int guass() { int c ,r; for (c = 0, r = 0; c < n; c++) { int t = r; for (int i = r; i < n; i++) if (fabs(a[i][c]) > fabs(a[t][c])) t = i; if (fabs(a[t][c]) < eps) continue; for (int i = c; i <= n; i++) swap(a[t][i], a[r][i]); for (int i = n; i >= c; i--) { a[r][i] /= a[r][c]; } for (int i = r + 1; i < n; i++) { if (fabs(a[i][c]) > eps) for (int j = n; j >= c; j--) a[i][j] -= a[r][j] * a[i][c]; } r++; } if (r < n) { for (int i = r; i < n; i++) { if (fabs(a[i][n]) > eps) return 2; } return 1; } for (int i = n - 1; i >= 0; i--) for (int j = i + 1; j < n; j++) a[i][n] -= a[i][j] * a[j][n]; return 0; } int main() { cin >> n; for (int i = 0; i < n; i++) for (int j = 0; j < n + 1; j++) cin >> a[i][j]; int t = guass(); if (t == 0) { for (int i = 0; i < n; i++) { printf("%.2f ",a[i][n]); } } else if(t==1){ printf("Infinite group solutions"); } else { puts("No solution"); } return 0; }

