面积最大的全1子矩阵--九度OJ 1497

题目描述：

在一个M * N的矩阵中，所有的元素只有0和1，从这个矩阵中找出一个面积最大的全1子矩阵，所谓最大是指元素1的个数最多。

输入：

输入可能包含多个测试样例。
对于每个测试案例，输入的第一行是两个整数m、n(1<=m、n<=1000)：代表将要输入的矩阵的大小。
矩阵共有m行，每行有n个整数，分别是0或1，相邻两数之间严格用一个空格隔开。

输出：

对应每个测试案例，输出矩阵中面积最大的全1子矩阵的元素个数。

样例输入：

2 2
0 0
0 0
4 4
0 0 0 0
0 1 1 0
0 1 1 0
0 0 0 0

样例输出：0 4

解题思路：转载自http://www.cnblogs.com/fstang/archive/2013/05/19/3087746.html

方法是：

1、先将0/1矩阵读入x，对每一个非零元素x[i][j]，将其更新为：在本行，它前面的连续的1的个数+1（+1表示算入自身）

　　比如，若某一行为0 1 1 0 1 1 1，则更新为0 1 2 0 1 2 3

2、对每一个非零元素x[i][j]，在第j列向上和向下扫描，直到遇到比自身小的数，若扫描了y行，则得到一个大小为x[i][j]*(y+1)的全1子矩阵（+1表示算入自身所在行）

　　比如，若某一列为[0 3 4 3 5 2 1]'(方便起见，这里将列表示成一个列向量)，我们处理这一列的第4个元素，也就是3，它向上可以扫描2个元素，向下可以扫描1个元素，于是得到一个4×3的全1子矩阵。

3、在这些数值中取一个最大的。

思想大概如下图所示（空白处的0没有标出）

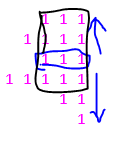
对照步骤2中给出的例子，蓝色的箭头表示向上向下扫描，黑色的框表示最终得到的全1子矩阵

这样做为什么是对的？

想一想，对那个最大的全1子矩阵，用这种方法能不能找到它呢？——肯定可以。

一个最大全1子矩阵，肯定是四个边界中的每一个都不能再扩展了，如下图

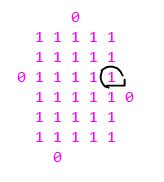
假设图中全1子矩阵就是最大子矩阵，则左边界左侧那一列肯定有一个或多个0（否则就可以向左边扩展一列，得到一个更大的全1矩阵）

对其他3个边界有类似的情况。

然后看图中用黑圈标出的1（其特点是：和左边界左侧的某个0在同一行），从这个1出发，按照之前的方法，向上向下扫描，就可以得到这个子矩阵。所以，肯定可以找到。

下面是我的代码，实际实现的时候，为了提高效率，估计了一下upperbound，这个upperbound就是：在当前列，

包含x[i][col]的连续的非零序列的和，比如对某列[0 3 4 3 5 2 1]'，后面6个的upperbound都是
3 + 4 + 3 + 5 + 2 + 1 = 18，对于0元素，不需要upperbound

#include<iostream>
using namespace std;

int main()
{
    int n,m;
    while(cin>>n>>m){
        int **array=new int*[n];
        int **upperbound=new int*[n];
        for(int i=0;i<n;i++){
            array[i]=new int[m];
            upperbound[i]=new int[m];
            for(int j=0;j<m;j++){
                cin>>array[i][j];
                upperbound[i][j]=0;
            }
        }
        //prepare:
        for(int i=0;i<n;i++){
            for(int j=1;j<m;j++){
                if(array[i][j]==1&&array[i][j-1]!=0)array[i][j]=array[i][j-1]+1;
            }
        }
        //计算upperbound
        for(int j=0;j<m;j++){
            for(int i=0;i<n;i++){
                if(array[i][j]==0)continue;
                else{
                    int sum=0,temp=i;
                    while(temp<n&&array[temp][j]>0){
                        sum+=array[temp][j];
                        temp++;
                    }
                    for(int k=i;k<temp;k++){
                        upperbound[k][j]=sum;
                    }
                    i=temp;
                }
            }    
        }

        int maxarea=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(array[i][j]!=0&&maxarea<upperbound[i][j]){
                    int cnt=1,val=array[i][j];
                    for(int row=i-1;row>0;row--){
                        if(array[row][j]>=val)cnt++;
                        else
                            break;//这里一定要break
                    }
                    for(int row=i+1;row<n;row++){
                        if(array[row][j]>=val)cnt++;
                        else
                            break;//这里一定要break
                    }
                    if(cnt*val>maxarea)maxarea=cnt*val;
                }
            }
        }
        cout<<maxarea;
    }
    return 0;
    
}