概率图的一个重要作用是进行推理,针对某个随机变量,告诉我们它到底有没有可能,有多大可能发生。之前在representation相关的内容中,我们更多的关心如何利用概率图减少联合分布的计算量。inference相关的章节就是要介绍如何从联合概率中获得单个随机变量的概率。
1.链状变量消除
对于给定的联合分布函数P(A,B,C,D,E),如果想要知道P(E),只需要将A,B,C,D边际掉。假设P(E)可以有两种取值P(e1),P(e2),P(e1) = P(a1,b1,c1,d1,e1)+P(a2,b1,c1,d1,e1)...以此类推,最终可以得到P(e1)与P(e2)的值。在有概率图的情况下,我们可以对变量进行因式分解,因式分解有助于减少求和的次数。
以如下图所示的链状无向图为例:

由马尔科夫图的团势分解定律可知,某个点的团仅与 其及其父节点有关,所以可以对上述联合概率进行因式分解。而仅 Φ(A,B)与A有关。把Φ(A,B)中的A边际掉,也就是T1(B1)=Φ(A1,B1)+Φ(A2,B1).T1(B2)=Φ(A1,B2)+Φ(A2,B2). 其结果相当于是一个仅与B取值有关的势函数。同理,这样已知进行下去可以得到仅与E取值有关的函数。

在有了这样的规则以及分布表达后,查询某个变量的概率实际上是非常简单的事情。
2.马尔科夫网的变量消除
对于一个如图所示的马尔科夫网,我们希望对P(J)进行计算。

P(C,D,I,G,S,L,J,H) = P(C)*P(C,D)*P(I)*P(DIG)*P(IS)*P(GL)*P(SLJ)*P(GJH)【这里的P应该表示为Φ】
如果要计算P(J),那么需要将C,D,I,G,S,L,H全部边际掉。也就是Sum_C,D,I,G,S,L,H P(C,D,I,G,S,L,J,H)
Sum_C,D,I,G,S,L,H P(C,D,I,G,S,L,J,H)
=Sum_C,D,I,G,S,L,H P(C)*P(C,D)*P(I)*P(DIG)*P(IS)*P(GL)*P(SLJ)*P(GJH)
=Sum_C,D,I,G,S,L P(C)*P(C,D)*P(I)*P(DIG)*P(IS)*P(GL)*P(SLJ)*Sum_H P(GJH)
=Sum_C,D,I,G,S,L P(C)*P(C,D)*P(DIG)*P(IS)*P(GL)*P(SLJ)*t(GJ)
=Sum_C P(C)*P(C,D)*Sum_D,I,G,S,L P(DIG)*P(IS)*P(GL)*P(SLJ)*t(GJ)
=Sum_D,I,G,S,L P(DIG)*P(IS)*P(GL)*P(SLJ)*t1(GJ)*t2(D)
=Sum_I,G,S,L P(IS)*P(GL)*P(SLJ)*t1(GJ) *Sum_D P(DIG)*t2(D)
=Sum_I,G,S,L P(IS)*P(GL)*P(SLJ)*t1(GJ)*t3(GI)
=Sum_G t3(GI)t1(GJ)P(GL) *Sum_ISL *P(SLJ)*P(IS)*t1(GJ)
=Sum_ISL P(SLJ)*t4(IJL)
按照此方法即可求出P(J).
3.变量消除的顺序
显然,变量消除的顺序会对算法的复杂程度产生巨大的影响。而好的变量消除顺序则显然与图的结构有关.还是以上一章节的图为例:
P(C,D,I,G,L,S,J,H) = P(C) P(D|C) P(I) P(G|DI) P(S|I) P(L|G) P(J|SL) P(H|GJ)
如果使用无向图的势函数表示,则表示为 P(C)*P(C,D)*P(I)*P(DIG)*P(IS)*P(GL)*P(SLJ)*P(GJH)【这里的P应该表示为Φ】
显然,这里需要做一些变化, DIG,GJH 是一个团,团里所有的节点应该是两两相连的。那么可得从贝叶斯有向模型推出对偶的无向图模型。

显然,可以以图中节点的顺序来进行消除,由外到内,先消除对结构影响小的再消除会带来结构改变的。这里的结构改变是指某一个变量消除后会得到t(****),这里的t(****)中每个变量应该是两两相连的。
所以,此图合适的消除顺序是 C D I H G S L。
4.消除顺序的计算机解法
实际上,对于一个复杂的图,不可能人为指定消除顺序。应该要有一套合适的算法或者评估机制来决定先消除哪个,后消除哪个。目前已经应用成功的消除顺序算法包括:
min-neighber: 某个点如果相连节点最少则优先消除(比如C)
min-weight : 对马尔科夫模型而言,消除因子值之和最小的的边
min-fill : 消除某个节点后,需要补充的边最少
weighted min-fill: 补充边的权重最小(边权重可作为两节点权重之积)
对于机器人定位这么一个实际问题,有如下图模型:
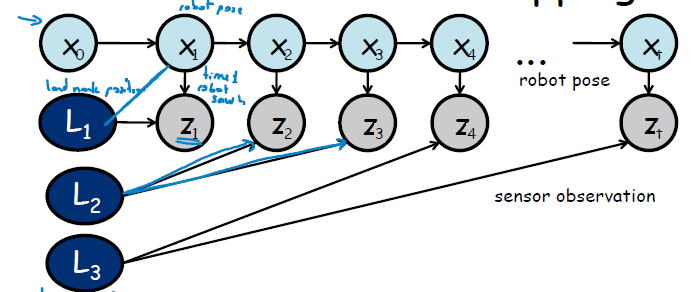
其中 x 是机器人的位置,z 是机器人观测到与标志物的距离, L 是标志物的位置。
从理想角度而言,标志物是固定的,观测距离一旦获得,那么机器人的位置就是确定的。但实际上不是,前面讨论过传感器是有测量误差的(近高斯模型),在考虑传感器测量误差的情况下,通过前后位置测量信息综合考虑,最后可以获得更为精确的地图。所以 Z 依赖于 L, X依赖于 Z。L 相当于一个观测值已知的随机变量,那么则可以把上图转为马尔科夫模型并构建概率图如下:



原始概率图:X,L 先消除X红色为补充边 先消除L 红色为补充边