PCL—低层次视觉—关键点检测（Harris）

　　除去NARF这种和特征检测联系比较紧密的方法外，一般来说特征检测都会对曲率变化比较剧烈的点更敏感。Harris算法是图像检测识别算法中非常重要的一个算法，其对物体姿态变化鲁棒性好，对旋转不敏感，可以很好的检测出物体的角点。甚至对于标定算法而言，HARRIS角点检测是使之能成功进行的基础。

　　HARRIS算法的思想还是很有意思的。很聪明也很trick.

1.Harris 算法　

　　其思想及数学推导大致如下：

　　

　　1.在图像中取一个窗 w (矩形窗，高斯窗，XX窗，各种窗，某师姐要改标定算法不就可以从选Harris的窗开始做起么。。。。。）

　　2.获得在该窗下的灰度  I

　　3.移动该窗，则灰度会发生变化，平坦区域灰度变化不大，边缘区域沿边缘方向灰度变化剧烈，角点处各个方向灰度变化均剧烈

　　4.依据3中条件选出角点

　　当然啦，如果Harris算子的实现也和它的思想这么平淡那我就不表扬他聪明了，Harris算子的具体实现方法，利用的是图像偏微分方程的思想。

　　先给出抽象数学表达式(不要问我为什么这么淡，我也不知道）：

　　其中 w 代表窗函数，某个x,y为图像坐标，u,v是一个移动向量（既反应移动方向，也反应移动大小）。

 

　　Ix表示图像沿x方向的差分，Iy表示图像沿y方向的差分。图像差分算子有什么Sober~PXX~总之很多就对了，一阶差分还是很好求的。

　　

　　显然，E(u,v)可以用另外一种形式来表示了。最终可以表达为协方差矩阵的形式。

　　OK，在这里我们有了数学中最优雅的表达——Matrix，especially symmetric Matrix. Nothing is better than that.

　　

2.矩阵的方向性

　　

　　显然，E(u,v)的值和u,v有关。。。很有关。。

　　1.可以取一组u,v，让E(u,v)的值最小。

　　2.还可以取一组u,v，让E(u,v)的值最大。

　　

　　这些u,v怎么取，显然就和矩阵M的方向有关了。OK，让我们换一个思路来看这个矩阵。

　　平面内的一个矩阵乘以一个向量v，大概简单的写成   Mv

　　它会使得这个向量发生一个作用：旋转，拉伸，平移.....总之，这种作用叫做  线性变换

　　矩阵的左边好像也是一个向量，只不过是横着写的（[u v]），换而言之，那就是 vT（v的转置）。

　　vT（Mv)......这是啥？

　　意思好像是。。。。v先旋转+拉伸一下，然后再在它自己身上投影，最终的 E(u,v)本质上来说，就是这个投影的长度。。。嗯，对，投影的长度

　　好了。我们现在明确了 E(u,v) 的数学几何意义，再回过头来想想，要怎样才能让这个投影的长度达到最大或者最小呢？

　　显然，答案就是矩阵的特征值与特征向量，当[u v]T 取特征向量方向的时候，矩阵M只有拉伸作用，而没有旋转作用，这时的投影长度是最长的（如果反向投则是负的最长）。

　　

　　到此为止，我们已经知道了 E(u,v）的最大和最小值了（笨办法是求出特征向量方向再带进去，聪明的方法是直接看矩阵特征值，特征值就是放大倍数）。并且，分析可以知道，特征值越大，那么说明 E(u,v)越大。

　　1.两个特征值都很大==========>角点（两个响应方向）

　　2.一个特征值很大，一个很小=====>边缘（只有一个响应方向）

　　3.两个特征值都小============>平原地区（响应都很微弱）

 

　　基于上述特征，有很多人设计了角点的快速判据。

　　有 det(M) - trace(M)^2

　　有 det(M)/trace(M)

　　.....等等很多，但是这不重要，思想都是一样的。（某师姐这里又有一个标定算法的创新点哦。。。。我会告诉你换换判据又是个新思路？）

　　

3. 3DHarris　

　　在2DHarris里，我们使用了 图像梯度构成的 协方差矩阵。 图像梯度。。。嗯。。。。每个像素点都有一个梯度，在一阶信息量的情况下描述了两个相邻像素的关系。显然这个思想可以轻易的移植到点云上来。

　　OOPS，糟糕，点云木有灰度的概念啊，一般的点云也木有强度的概念啊。。。这可如何是好？？？？？？

　　别紧张，pcl 说这样能行，那就肯定能行咯，先定性的分析一下Harris3D的理念。

　　想象一下，如果在 点云中存在一点p

　　1、在p上建立一个局部坐标系：z方向是法线方向，x,y方向和z垂直。

　　2、在p上建立一个小正方体，不要太大，大概像材料力学分析应力那种就行

　　3、假设点云的密度是相同的，点云是一层蒙皮，不是实心的。

　　　　a、如果小正方体沿z方向移动，那小正方体里的点云数量应该不变

　　　　b、如果小正方体位于边缘上，则沿边缘移动，点云数量几乎不变，沿垂直边缘方向移动，点云数量改变

　　　　c、如果小正方体位于角点上，则有两个方向都会大幅改变点云数量

　　OK，我们已经有了Harris3D的基本准则，接下来要思考的是怎样优雅的解决这个问题

　　

　　两个和z相互垂直的方向。。。。嗯。。。。perpendicular。。。。

　　如果由法向量x,y,z构成协方差矩阵，那么它应该是一个对称矩阵。而且特征向量有一个方向是法线方向，另外两个方向和法线垂直。

　　那么直接用协方差矩阵替换掉图像里的M矩阵，就得到了点云的Harris算法。

　　其中，半径r可以用来控制角点的规模

　　r小，则对应的角点越尖锐（对噪声更敏感）
　　r大，则可能在平缓的区域也检测出角点

　　r怎么取？ 我也不知道。。。。。试吧。。。。。

 

 4.PCL对Harris算法的实现

　　根据以上分析，在PCL的API文档的帮助下，我尝试了一下 Harris3D 算法。感谢山大的毕同学提供的点云，该点云是场景点云而不是一般的物体点云。总体感觉是慢，因为针对每个点云，需要计算它的法线，算完之后又要针对每个点进行协方差矩阵的计算，总而言之，整个过程还是非常耗时的。并且说实话。。。算法的效果一般般。

　　

#include <iostream>
#include <pcliopcd_io.h>
#include <pcl/point_cloud.h>
#include <pcl/visualization/pcl_visualizer.h>
#include <pcl/io/io.h>
#include <pcl/keypoints/harris_keypoint3D.h>
#include <cstdlib>
#include <vector>
using namespace std;



int
main()
{
    pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>);
    pcl::io::loadPCDFile ("F:\PCL\PCD\both.pcd", *cloud);
    boost::shared_ptr<pcl::visualization::PCLVisualizer> viewer(new pcl::visualization::PCLVisualizer);
    viewer->addPointCloud(cloud,"all_cloud");
        //注意Harris的输出点云必须是有强度(I)信息的，因为评估值保存在I分量里
    pcl::PointCloud<pcl::PointXYZI>::Ptr cloud_out (new pcl::PointCloud<pcl::PointXYZI>);
    pcl::HarrisKeypoint3D<pcl::PointXYZ,pcl::PointXYZI,pcl::Normal> harris;
    harris.setInputCloud(cloud);
    cout<<"input successful"<<endl;
    harris.setNonMaxSupression(true);
    harris.setRadius(0.04f);
    harris.setThreshold(0.02f);
    cout<<"parameter set successful"<<endl;
        //新建的点云必须初始化，清零，否则指针会越界
    cloud_out->height=1;
    cloud_out->width =100;
    cloud_out->resize(cloud_out->height*cloud->width);    
        cloud_out->clear();
    harris.compute(*cloud_out);
    int size = cloud_out->size();

    pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_harris (new pcl::PointCloud<pcl::PointXYZ>);
    cloud_harris->height=1;
    cloud_harris->width =100;
    cloud_harris->resize(cloud_out->height*cloud->width);
    cloud_harris->clear();

    pcl::PointXYZ point;
        //可视化结果不支持XYZI格式点云，所有又要导回XYZ格式。。。。
    for (int i = 0;i<size;i++)
    {    
        point.x = cloud_out->at(i).x;
        point.y = cloud_out->at(i).y;
        point.z = cloud_out->at(i).z;
        cloud_harris->push_back(point);
    }



    pcl::visualization::PointCloudColorHandlerCustom<pcl::PointXYZ> harris_color_handler (cloud_harris, 0, 255, 0);
    viewer->addPointCloud(cloud_harris,harris_color_handler,"harris");
    viewer->setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 5, "harris");




    while (!viewer->wasStopped())
    {
        viewer->spinOnce(100);

    }
    
        system("pause");
}    

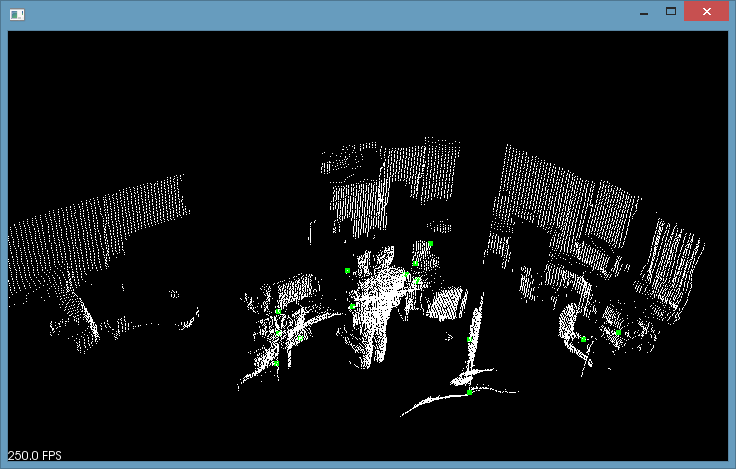
　　由于我选择的搜索半径比较大，所以找到的角点都不是太"角”,关于参数设置大家可以多多探索，但我认为，特征点检测算法实在太慢，对实时机器人系统来说是远远达不到要求的。这种先算法线，再算协方差的形式真心上不起。。。。实际上这种基于领域法线的特征点检测算法有点类似基于 CRF的语义识别算法，都只使用了相邻信息而忽略了全局信息。也可能相邻信息包含的相关性比较大，是通往高层次感知的唯一路径吧，谁又知道呢？

　　任重而道远。。。。。