输出"魔方阵" 所谓魔方阵是指这样的方阵，它的每一行、每一列和对角线之和均相等。例如：

输出"魔方阵"。所谓魔方阵是指这样的方阵，它的每一行、每一列和对角线之和均相等。例如：

8   1   6
3   5   7
4   9   2

要求输出1~(n^2)的自然数构成的魔方阵。

【答案解析】

| 17 | 24 |  1 |  8 | 15 |
--------------------------
| 23 |  5 |  7 | 14 | 16 |
--------------------------
|  4 |  6 | 13 | 20 | 22 |
--------------------------
| 10 | 12 | 19 | 21 |  3 |
--------------------------
| 11 | 18 | 25 |  2 |  9 |

仔细观察上述矩阵，可以看到以下规律：

魔方阵的生成方法为：在第0行中间置1，对从2开始的其余(n^2-1)个数依次按下列规则存放：

1. 将1放在第1行的中间一列。
2. 从2开始直到n*n止，各数依次按此规律存放：每一个数存放的行比前一个数的行数减1，列数加1。
3. 如果上一行的行数为1，则下一个数的行数为n(指最下一行）。
4. 当上一个数的列数为n时，下一个数的列数应该为1。
5. 如果按上面规律确定的位置有数，或者上一个数是第1行第n列时，则把下一个数放在上一个数的下面。

【代码实现】

#include <stdio.h>
int main()
{
	int a[15][15], n, i, j, k;
	while (1)
	{
		printf("请输入n(1~15):");
		scanf("%d", &n);
		if (n != 0 && n <= 15 && n % 2 != 0)
			break;
		else
		{
			printf("请输入奇数
");
		}
	}

	for (i = 1; i <= n; i++)
	{
		for (j = 1; j <= n; j++)
			a[i][j] = 0;
	}

	j = n / 2 + 1;
	a[1][j] = 1;
	i = 1;
	for (k = 2; k <= n*n; k++)
	{
		i -= 1;
		j += 1;

		if (i<1 && j>n)
		{
			i += 2;
			j -= 1;
		}
		else if (i<1)
		{
			i = n;
		}
		else if (j>n)
		{
			j = 1;
		}

		if (a[i][j] == 0)
		{
			a[i][j] = k;
		}
		else
		{
			i += 2;
			j -= 1;

			a[i][j] = k;
		}
	}

	for (i = 1; i <= n; i++)
	{
		for (j = 1; j <= n; j++)
			printf("%5d", a[i][j]);

		printf("
");
	}

	return 0;
}

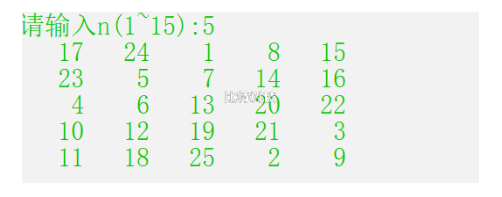
【结果截屏】