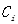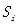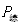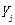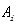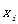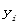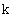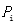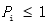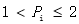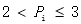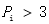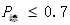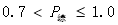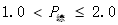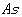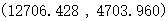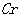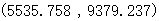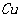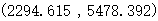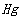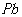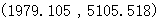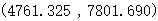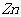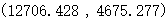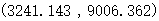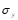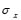城市表层土壤重金属污染问题分析
摘 要:本文针对城市表层土壤重金属的污染问题,运用数据分析和建立数学模型的方法,在MATLAB、SPSS、EXCEL等软件的帮助下,解决了分功能区分析城市表层土壤重金属污染原因、寻找污染源头的问题,具体如下:
针对问题一,我们首先借助MATLAB软件,将附件中提供的坐标点对应数据插值扩充数量后的海拔高度作图,得出相对于水平空间分布,垂直空间分布的差异不是很明显,又考虑到我们研究的是城市表层土壤,海拔高度对不同坐标点的土壤中金属污染元素的含量的影响很小,所以可以简化空间概念,假定为二维空间;然后根据附件中提供的每个点的空间坐标及其所对应的每种元素的浓度,分别作出8种元素的空间分布图,最后引入內梅罗综合指数法,根据图像对所研究城区的不同区域的污染程度进行分析。
针对问题二,我们首先借助EXCEL和SPSS进行均值、标准偏差、峰度、最值、偏度等统计数据的计算及表格制作,通过分析对比得出不同坐标点的金属元素浓度差异太大,如果用浓度平均值进行计算分析会产生很大的误差,所以用每个坐标点对应的金属元素浓度进行计算,然后我们通过SPSS软件进行重金属污染元素在各个功能区的浓度进行主成分分析法,得出每个功能区的主要污染元素,最后根据每个功能区的特点分析产生污染的原因。
针对问题三,我们首先沿用问题一Kringing插值法后的1000×1000个数据点,然后利用元胞的思想为每一种元素筛选出60-100个浓度极大值,再进一步在这些点中取出一定个数的、比较大的元素浓度值以及其所对应的坐标点,最后利用MATLAB软件进行拟合,找出拟合度最接近1的点,以此作为污染源。
针对问题四,我们首先分析前三问中模型的优缺点,其次考虑实际因素,确定需要额外收集的数据信息为风速、风向和时间,然后引入高斯烟羽模型,最后根据实际研究方向以及研究范围进行模型的修改进行问题的求解。
关键词:Kringing插值法 内梅罗综合指数法 主成分分析 高斯烟羽模型
1问题重述
城市经济的快速发展和城市人口的不断增加致使人类活动对城市环境质量的影响日显突出。对城市土壤地质环境异常的查证,以及如何应用查证获得的海量数据资料开展城市环境质量评价,研究在人类活动影响下城市地质环境的演变模式,日渐成为人们关注的焦点。
按照功能划分,将城区分为生活区、工业区、山区、主干道路区及公园绿地区等,分别记为1类区、2类区、……、5类区,不同的区域环境受人类活动影响的程度不同。
现对某城市城区土壤地质环境进行调查。为此,将所考察的城区划分为间距1公里左右的网格子区域,按照每平方公里1个采样点对表层土(0~10 厘米深度)进行取样、编号,并用GPS记录采样点的位置。应用专门仪器测试分析,获得了每个样本所含的多种化学元素的浓度数据。另一方面,按照2公里的间距在那些远离人群及工业活动的自然区取样,将其作为该城区表层土壤中元素的背景值。
现需根据附件中所给定的数据,建立数学模型解决以下问题:
问题一:
给出8种主要重金属元素在该城区的空间分布,并分析该城区内不同区域重金属的污染程度。
问题二:
通过数据分析,说明重金属污染的主要原因。
问题三:
分析重金属污染物的传播特征,由此建立模型,确定污染源的位置。
问题四:
分析你所建立模型的优缺点,为更好地研究城市地质环境的演变模式,还应收集什么信息?有了这些信息,如何建立模型解决问题?
2基本假设与符号说明
2.1基本假设
①假设在我们研究的过程中城区内静止无风;
②假设数据表插值之后的所有数据点均具有研究价值;
③假设取样点的数据能够很好的反映该城区内各功能区的属性;
④假设重金属污染元素的浓度在调查期间没有大幅度的变化;
⑤假设金属污染不考虑植树吸收,表现为富集形式;
⑥假设各地区重金属分布稳定,污染源排放量固定不变。
2.2符号说明
|
|
表示第i种重金属元素的污染指数 |
|
|
表示第i种重金属元素含量的实测值,即浓度 |
|
|
表示第i种重金属元素的背景值 |
|
|
表示內梅罗综合指数 |
|
|
表示提取的主成分对第j种元素的载荷 |
|
|
表示第i个主成分的方差百分比 |
|
|
表示第i个主成分对第j种元素的载荷 |
|
|
表示第i个污染源的x坐标 |
|
|
表示第i个污染源的y坐标 |
|
|
表示扩散系数 |
|
|
表示扩散半径 |
3问题分析
问题一:对于问题一,第一步是需要根据附件中提供的每个坐标点的海拔高度进行插值,扩充数据量后进行作图分析,确定所研究的空间维度。第二步是根据所提供数据中不同坐标点对应的每种元素的浓度做出元素空间分布图。第三步是操作附件种的数据,利用单因子指数和內梅罗综合指数法分析不同区域土壤重金属的污染程度。
问题二:对于问题二,首先考虑到题目将所研究的城区分为生活区、工业区、山区、主干道路区及公园绿地区等物种类型,各区之间主要差别在于自然地理条件不同以及人类生活足迹不同,所以我们首先将重金属污染的原因分为自然因素和人为因素两种;其次我们需要根据附件2中所提供的主要重金属元素的浓度找出不同功能区中污染土壤的主要元素,在综合各功能区的工作特点的基础上,分析每种功能区对应的主要重金属污染元素的产生原因,进而得以说明重金属污染产生的主要原因。
问题三:对于问题三,首先确定重金属元素的传播特点大致符合自然界规律,即从高浓度向低浓度传播,同时注意到重金属元素传播速度比较慢且不同元素传播速度不同,将此题分元素进行求解;其次建立元素传播模型,同时通过元胞的思想进行数据点的初步筛选,然后进一步筛选出数量更少的符合我们预期的数据点,利用MATLAB软件与元素传播模型进行拟合,找出拟合度最接近1的坐标点作为该元素的传播源。
问题四:对于问题四,首先需要根据前三问模型的建立与求解确定出我们研究还需要收集的数据信息,为更好的研究地质环境演变模式,引入新的模型,并考虑实际研究情况进行模型的修改修订,最终解决问题。
4模型的建立与求解
4.1问题一模型的建立与求解
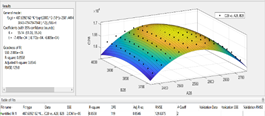
对于问题一,我们希望尽量降低空间维度来简化问题,首先运用MATLAB软件做出海拔分布图,如图1
图1 坐标点海拔分布图
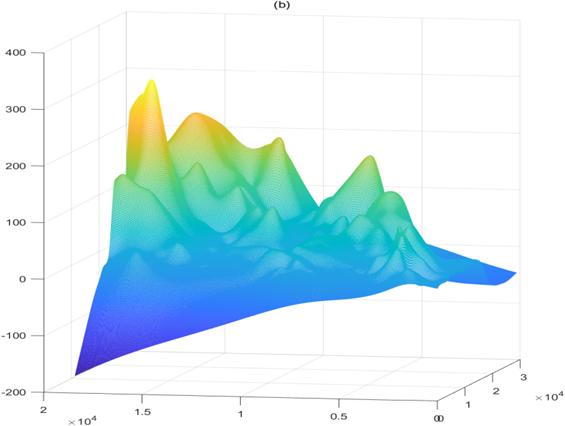
从图中可以得出x坐标和y坐标的量级均是z坐标的100倍以上,同时因为我们研究的是城区表层土壤的重金属污染程度,表层土壤是指地表下厚度为26-28cm左右范围内的土壤,而数据中各坐标点的海拔高度也是这个值的100倍以上,所以我们忽略海拔高度对表层土壤中重金属污染元素浓度的含量的影响,将研究空间降为二维平面。
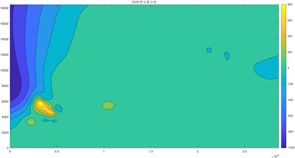
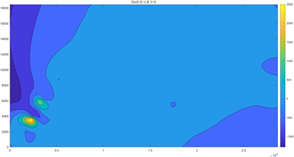
然后我们根据附件中给出的319个坐标点对应的每种元素的浓度作图:
|
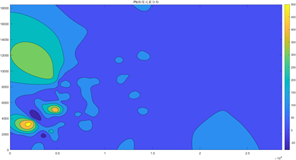
图2 As元素空间分布图
|
图3 Cd元素空间分布图
|
|
图4 Cr元素空间分布图
|
图5 Cu元素空间分布图
|
|
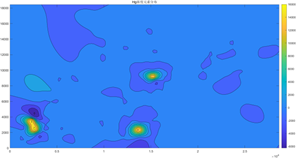
图6 Hg元素空间分布图
|
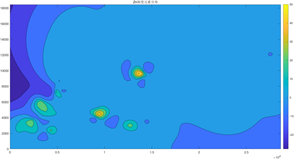
图7 Ni元素空间分布图
|
|
图8 Pb元素空间分布图
|
图9 Zn元素空间分布图
|
以上8张图是8种元素的污染空间分布图,图中亮黄色和橙色的部分为该图对应的重金属污染元素浓度比较高的区域,可以从图中看出受每种元素污染程度比较严重的地理区域。
我们引入单因子指数的概念:

计算出8种元素分别在319个坐标点上的污染指数,计算结果由附件1种的工作表1给出,并根据土壤单项污染程度分级标准标记每种元素在每个坐标点上的污染程度。
表1 土壤单项污染程度分级标准
|
|
|
|
|
|
|
污染水平 |
非污染 |
轻污染 |
中污染 |
重污染 |
考虑到我们需要分析所研究城区内不同区域的污染程度,是需要综合8种重金属污染元素的影响来分析,所以引入內梅罗综合指数进行进一步的分析:
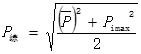
在计算出319个坐标点的综合指数后,根据土壤综合污染程度分级标准标记每个坐标点的土壤污染程度。
表2 土壤综合污染程度分级标准
|
土壤综合污染等级 |
土壤综合污染指数 |
污染程度 |
污染水平 |
|
1 |
|
安全 |
清洁 |
|
2 |
|
警戒线 |
尚清洁 |
|
3 |
|
轻污染 |
开始产生污染 |
|
4 |
|
中污染 |
污染明显 |
|
5 |
|
重污染 |
污染严重 |
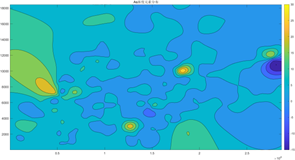
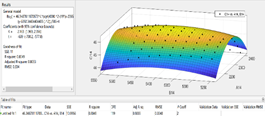
根据所求得的综合指数,利用MATLAB软件绘制出各个坐标点的综合指数分布图,如图10。
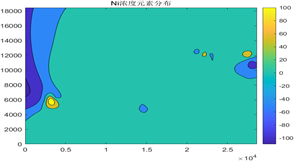
图10 综合指数空间分布图
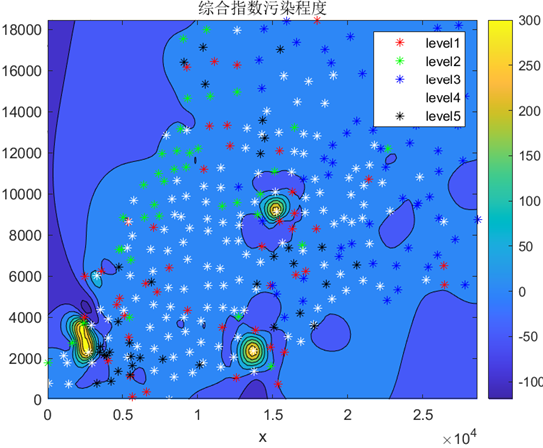
由图可以得出:所研究城区内土壤重金属污染程度有明显的区域差异,图中三个明显的亮黄色区域是土壤污染综合指数最高的区域,即污染比较严重的区域,而三个重污染区周围分布的从橙黄色到蓝绿色的区域则为污染比较轻的区域。
图中level1表示生活区,level2表示 工业区,level3表示山区,level4表示主干道路区,level5表示公园绿地区,由图中的坐标点在综合指数分布图种的位置可以得出,我们所研究的城区种污染比较严重的区域是工业区和主干道路区。
4.2问题二模型的建立与求解
对于问题二,需要找出污染产生的主要原因,我们通过SPSS和EXCEL进行计算,得出每种元素在全区内浓度值的各种统计值如表3:
表3 土壤重金属元素浓度统计分析
|
元素 |
As (μg/g) |
Cd (ng/g) |
Cr (μg/g) |
Cu (μg/g) |
Hg (ng/g) |
Ni (μg/g) |
Pb (μg/g) |
Zn (μg/g) |
|
背景值 |
3.60 |
130.00 |
31.00 |
13.20 |
35.00 |
12.30 |
31.00 |
69.00 |
|
最大值 |
30.13 |
1619.80 |
920.84 |
2528.48 |
16000.00 |
142.50 |
472.48 |
3760.82 |
|
标准偏差 |
0.90 |
30.00 |
9.00 |
3.60 |
8.00 |
3.80 |
6.00 |
14.00 |
|
平均值 |
5.68 |
302.40 |
53.51 |
55.02 |
299.71 |
17.26 |
61.74 |
201.20 |
|
变异系数 |
0.16 |
0.10 |
0.17 |
0.07 |
0.03 |
0.22 |
0.10 |
0.07 |
|
中值 |
5.31 |
238.70 |
42.02 |
27.98 |
50.00 |
15.98 |
45.83 |
106.43 |
|
最小值 |
1.61 |
40.00 |
15.32 |
2.29 |
8.57 |
4.27 |
19.68 |
32.86 |
|
偏度 |
3.32 |
2.02 |
9.45 |
12.76 |
8.60 |
7.11 |
4.41 |
6.49 |
|
峰度 |
19.70 |
5.64 |
104.17 |
180.69 |
74.15 |
81.84 |
28.31 |
53.59 |
从表中得出,所研究的地区的土壤中每种重金属元素含量的最大值与最小值差异是几十倍,如果用浓度平均值进行计算分析会产生很大的误差,所以我们采用单个坐标点对应的重金属污染元素浓度进行计算。
通过对319个坐标点数据中对应每个功能区的重金属元素浓度进行主成分分析发,分别得出每个区域的各个成分的总方差贡献率,在附件2中给出,并利用SPSS主成分分析的碎石图选定每个功能区的成分矩阵,同样在附件2中给出。
根据公式
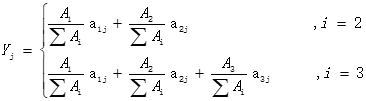
计算出每个功能区中提取出来的主成分对各重金属元素的总影响程度如下表
表4 各功能区每种重金属的污染贡献
|
As |
Cd |
Cr |
Cu |
|
|
生活区 |
0.2883 |
0.4428 |
0.5360 |
0.4089 |
|
工业区 |
0.5636 |
0.6578 |
0.7052 |
0.6087 |
|
山区 |
0.2600 |
0.2976 |
0.1883 |
0.4187 |
|
主干道路区 |
0.2812 |
0.5903 |
0.4954 |
0.5440 |
|
公园绿地区 |
0.3196 |
0.4724 |
0.3925 |
0.4877 |
续表4:
|
Hg |
Ni |
Pb |
Zn |
|
|
生活区 |
0.2505 |
0.4734 |
0.4563 |
0.4947 |
|
工业区 |
0.5910 |
0.7039 |
0.7038 |
0.7311 |
|
山区 |
0.4087 |
0.1454 |
0.3416 |
0.3056 |
|
主干道路区 |
0.3919 |
0.5296 |
0.5830 |
0.6206 |
|
公园绿地区 |
0.3501 |
0.2702 |
0.6130 |
0.5060 |
将上表转化为如下条形统计图:
图11 各功能区每种重金属的污染贡献
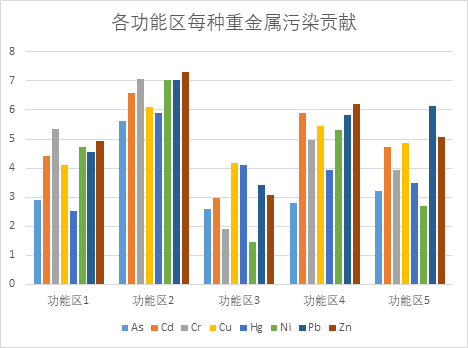
从图中可以直观的看出每个区域中主要的几种重金属污染元素:
表5 各功能区主要重金属污染元素
|
污染贡献元素 |
主要污染元素 |
|
|
生活区 |
Cr、Zn、Ni、Hg、Cd |
Cr |
|
工业区 |
Zn、Cr、Hg、Ni |
Zn |
|
山区 |
Cu、Hg |
Cu |
|
主干道路区 |
Zn、Cd、Hg |
Zn |
|
公园绿地区 |
Hg、Zn、Cu、Cd |
Hg |
通过上述数据分析结果,得出重金属污染产生的主要原因有:
①运输、冶金、建筑材料生产等产生的含有重金属的气体和粉尘进入大气,通过自然沉降和降水进入土壤,同时含铅汽油的燃烧和汽车轮胎磨损产生的粉尘对大气和土壤造成Zn、Cd、Cr、Cu等污染,主要产生与工业区和主干道路区,但由于生活区和公园绿地区与其临近,长期迁移的情况下,也受到了很大程度的污染。
②工业固体废弃物堆放和处理过程中,在日晒和雨淋等自然因素的影响下,极易使其中富含的重金属元素如Zn、Cr、Cu等发生移动,以辐射状、漏斗状向周围土壤、水体扩散,与工业区比较临近的主干道路区和生活区都会受到污染的影响。
③未经处理的工矿企业污水排入下水道,与生活污水混合,造成污水灌溉区土壤重金属Hg、Cr、Pb、Cd等的含量在长时间的沉积下远远超过其背景值,
④农药、化肥等长期的不合理使用,杀真菌的农药中含有Cu、Zn等重金属元素,倍大量的用于果树种植等地方,造成土壤中Cu、Zn的累积浓度超过背景值,成为了山区、公园绿地区的污染原因。
综合分析,不同程度的人类活动造成的污染直接或者通过自然沉降间接造成了城区不同功能区的重金属污染。
4.3问题三模型的建立与求解
金属元素的传播特点大致符合高浓度向低浓度传播的规律,同时重金属元素传播速度比较慢且不同元素传播速度不同,所以本题的模型建立与求解分元素进行。
运用元胞的思想将每种元素对应的1000×1000个数据点进行筛选,因为污染源的元素浓度显然会高于扩散区域内任意一点,所以进一步缩小范围,分别选择位于每种元素的空间分布图上污染程度严重区域的点。用目标点周围11×11的矩阵(附件3)与元素扩散模型进行拟合:
模型建立:
我们假设土壤中重金属元素的扩散是向以污染源为中心、扩散半径长度为半径的圆形在土地上方的半球体扩散,经过足够久的时间浓度不再发生大的变化,土地每个点垂直上方的元素全部垂直沉降至土地上对应的点且不再移动:
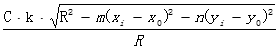
注:
①C表示污染源处的元素浓度
②模型中m和n是考虑到x轴方向和y轴方向上的扩散速度不同而修正模型引入的速度参数
得出拟合度相对比较高的点如下:
图12 As元素污染源坐标点与传播模型的拟合图
|
|
|
|
|
|
|
|
图13 Cd元素污染源坐标点与传播模型的拟合图
|
|
|
|
|
|
|
|
图14 Cr元素污染源坐标点与传播模型的拟合图
|
|
|
|
|
图15 Cu元素污染源坐标点与传播模型的拟合图
|
|
|
图16 Hg元素污染源坐标点与传播模型的拟合图
|
|
|
|
|
图17 Ni元素污染源坐标点与传播模型的拟合图
|
|
|
图18 Pb元素污染源坐标点与传播模型的拟合图
|
|
|
图19 Zn元素污染源坐标点与传播模型的拟合图
|
|
|
最终我们确定8种元素的污染源分别为:
|
元素 |
污染源坐标点 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.4问题四模型的建立与求解
首先考虑到前三问中模型的条件限制过于理想,此问中我们考虑一定数量的自然因素,引入风速、风向和时间的数据,并根据研究内容确定用高斯烟羽模型进行求解,采用大空间连续点源的高斯扩散模式:
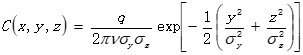
考虑实际研究方向,将模型修改如下:
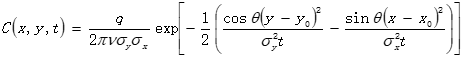
注,式中符号表示:
|
|
表示y轴扩散参数 |
|
|
表示x轴扩散参数 |
|
|
表示风速 |
|
|
表示风向与x轴的家教 |
|
|
表示源强,即单位时间内排放的污染物 |
|
|
表示扩散所经历的时间 |
5模型总结
本文的模型建立与模型求解主要有以下几个优点:
1.运用了Kringing插值法进行数据量的扩充,有助于优化图像;
2.在问题二中引入了内梅罗综合指数的概念进行土壤污染程度的界定,使得结果具有一定的参考价值;
3.在建立问题三的模型时采用元胞的思想对大量的数据进行了筛选,选择出了比较具有代表性的取样点,使得最终的结果更加精确。
但是在理论与实际结合的过程中考虑的因素仍有不足,所以还存在以下几点不足:
1.由于问题所给附件中的数据量有限,虽然采用了Kringing插值法进行数据量的扩充,但是由于其对数据具有代表性的要求比较高,使得模型的应用范围不够广;
2.问题二中引入的內梅罗综合指数过分强调污染浓度高的元素对于污染程度的贡献,可能导致最终结果具有一定的偏差。
3.问题三的模型是比较理想化的,没有考虑更多的气象因素和自然演变因素,所以导致模型的应用范围不够广;
参考文献
[1]唐家德.应用MATLAB绘制三维地貌图[J].现代计算机(专业版),2017(30):31-36.
[2]沈惠雅. 土壤重金属时空一体化数据异常识别研究[D].北华航天工业学院,2020.
[3]. 谢中华,夏国坤《城市表层土壤化学元素污染传播的核回归模型》
中图分类号:X53 文献标志码:A 文章编号:1672-6510(2012)06-0074-05
[4]. 苏鹏方 《大气污染成因分析及传播路径推演方法研究》
[5]. 史宝军,聂士明,孙静 《基于高斯烟羽混合模型的LPG泄漏扩散研究》 工程科技Ⅰ辑 DOI:10.13637/j.issn.1009-6094.2020.1517
[6]. 孙瑜 《基于高斯烟羽模型的一甲胺泄漏分析》工程科技Ⅰ辑 TQ086.52
[7]. 王学军,席爽.北京东郊污灌土壤重金属含量的克立格插值及重金属污染评价[J].中国环境科学,1997,17(3):225一228.
[8].祝红芳,王从庆,柏林,《机器人路径规划的元胞自动机算法》[J].江西:江西科学,第27卷第一期,36-40,2009.2
附录:本次模型建立与求解过程中的程序另见文件
结语:幸亏是早9的培训,照我们的黄sir来说就是957的生活,额滴神呐,这篇论文虽然有很多可以参考的优秀论文,但是自己动手又是另外一种感觉,有很多方法,但是不知道该用哪种方法,我们甚至讨论起来想要简单点还是难点,xswl,不过这都是敲代码的我来解决的,幸亏有先人指路,我的代码又很大部分都是参考他们的,虽然说这篇几乎用不到他们的代码哈,后面那个魔鬼物理题才是真正的折磨人,队友黄sir和纪sir也是一个比一个靠谱,虽然都是新手,但是。。。。。。这里自己想词吧hhhh
代码:Modeling/城市土壤污染 at master · instead-everyone/Modeling (github.com)