在做博弈模型评估的时候,遇到一个问题是如何评价多个模型的优劣。例如我有训练好的三个围棋模型A,B,C,两两之间对打之后有一个胜负关系,如何对这三个模型进行排序呢?通常对于人类选手这种水平有波动的情形,棋类比赛通常计算选手Elo得分按分值排序,足球篮球等通过联赛积分或胜场进行排序,但对于固定不变的AI模型,我认为用类似PageRank的方式计算更方便也更加准确。
这篇文章先从问题来源讲起,再讲解PageRank算法的思想,最后编程实现排序方法并指出一些需要注意的地方。
目录
一、问题来源
现在,深度强化学习更多的用在博弈模型的训练当中,比如围棋的AlphaZero,星际争霸的AlphaStar,DOTA的OpenAI FIVE。比如我们已经训练好了三个模型A,B,C,并且可以相互对打很多局,我们需要一个方法排出谁第一,谁第二。之前NeurIPS2019多智能体竞赛设计的排序方法就存在明显的bug,出现了A能胜过B,且A对C的胜率高于B对C的胜率,最后算出的排名却是B更靠前。主办方也承认了计算方式有缺陷并表示会在之后的比赛中修正,但是当前排名维持不变。
那为什么成熟的Elo值计算方式没有用在这类模型评估上面呢?Elo值通常用在围棋、象棋等棋类排名上,电子竞技例如英雄联盟等也可以认为是类似Elo的积分方式。这类问题的特点是
- 可通过一对一比赛得到一局的胜负关系,但和相同对手的对局次数有限,很难得到稳定的胜率关系。
- 玩家水平并非固定不变,可随环境、状态等因素波动(临场发挥),也可因长期训练/荒废而提升/下降(绝对实力)。
我们需要根据这种1v1(or 5v5)的每一局的胜负关系,给出所有玩家的即时能力大小排序。由于每个人的水平都会因为身体因素、年龄因素等产生波动,这和一个固定的模型是不一样的。而Elo可以根据每一局的实时对局结果立即更新当前排名,对棋类、竞技体育等的时效性需求非常适合,也可以较为准确的反应玩家的当前水平排名。虽然它也不是绝对的准确,不过已经是针对这类需求很好的排序方法了。
回过头来,对于已经训练好的AI模型,它的能力不会发生变化,并且我们可以通过足够多的测试得到两两之间的准确胜率关系,这种情况下我们如果强行套Elo的算法一局一局挑选对手对打,更新Elo值,再挑对手对打,再更新Elo值,就会显得没有必要(因为我们并不关心每一局后的实时排名)而且很麻烦,再者如果中途有一个新加入的模型需要从0开始评估,要想得到较为稳定的排名关系就会显得更加麻烦。
而PageRank的方法可以充分利用模型之间容易得到的稳定胜负关系,用矩阵迭代的方式计算出最终排名,简单且准确。
二、PageRank算法
算法思想
PageRank算法是Google发明用来做网页排序的,依据网页之间的链接关系对网页重要度进行排序。其主要设计思想如下
- (1) 每个网页的初始重要程度相同,比如(a=1,b=1,c=1,...)
- (2) 如果许多网页(b,c,d...)指向某个网页(a),则网页(a)很重要
- (3) 如果某个重要的网页(a)指向某个网页(b),则网页(b)因为(a)很重要也会获得更高的重要度。
这个想法其实和paper的引用有相似之处,每一篇新paper刚发表,很难评价其质量,可以粗略认为paper质量都一样;如果有一篇paper被引用很多,那么这篇paper肯定质量比较好;如果某偏很好的paper引用了另一篇paper,那这篇被引用的paper也理应质量不错。
基于这三点主要思想,我们假定有a,b,c,d四个网址,其链接关系如图所示
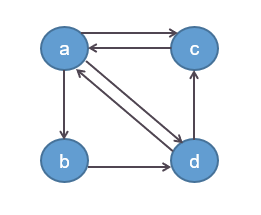
首先根据思想(1),假定每个网页的初始重要度相同,比如都是1,则有重要度向量(x=(1,1,1,1))。
接下来我们根据思想(2)、(3)计算每个网页被指向后的重要度变化。令(T_{i,j})表示网页(j)是否指向网页(i),则有
其中(i,j in {a,b,c,d}),且自己指向自己记为0,即(T(i,i)=0)。重要度的变化如下计算(x_i=sum x_j imes T_{i,j}),这种方式也很直觉,就是把所有指向(i)的网页的当前重要度加起来,就是网页(i)的重要度。由于刚开始大家的初始重要度都是1,则从图中的指向关系可以算出
同理有(x^prime(b)=1;x^prime(c)=3;x^prime(d)=2)。这里有一个问题需要注意,大家的初始权值都为1,但是发出去的权重却大于1,例如网页(a)指向了(b,c,d)三个网页,它发出去的权值为3,这是不太合理的。一个简单的修正方式是,令(T_{i,j})中同一个网页发出去的链接的和为1,从而每个(T_{i,j})还表示发出去的权值,而不仅仅表示有无。即有
此时,我们有(T_{i,a}=frac{1}{3};T_{i,b}=frac{1}{2};T_{i,c}=1;T_{i,d}=frac{1}{2})。重新计算每个网页的重要度有
同理有(x^prime(b)=frac{1}{3};x^prime(c)=frac{4}{3};x^prime(d)=frac{5}{6})。我们继续将重要度向量(x)进行第二次迭代计算,有
同理有(x^{primeprime}(b)=frac{1}{2};x^{primeprime}(c)=frac{13}{12};x^{primeprime}(d)=frac{2}{3})。将计算表示为矩阵形式,我们有
那么前两次迭代可以表示为
经过无穷次迭代(x^infty=T^infty x)收敛,(x^infty)每个分量的大小即为对应网页的重要度大小。实际情况中,不必作无限次运算即可收敛。
接下来的问题是:对于任意这样的矩阵,是否都会收敛呢?如何判断当前矩阵是否具有这种收敛性?下一步给出比较直观的理解和判断方法,忽略证明过程。
数学原理
如果我们把这个问题看作一个马氏(随机)过程,那么四个网页组成的向量(x)其实就是四个状态。我们不取权值1,而是归一化为(x=(frac{1}{4},frac{1}{4},frac{1}{4},frac{1}{4})),那么(x)可以看做是该马氏过程的初始状态概率分布。矩阵(T)就是一步的状态转移概率矩阵。我们的目标则是求该转移矩阵的平稳分布,这个平稳分布是与初始状态分布(x)无关的,也就是说无论(x)的取值是多少,最后算出来的(x^infty)都一样。那么现在的问题是什么样的(T)可以保证平稳分布存在且唯一。这里我们给出结论并简单解释,不作数学证明,可参考马氏链平稳分布存在与唯一性的简洁证明与计算。
定理: 若马氏链不可约且正常返,则平稳分布存在且唯一。
- 不可约:通俗来说,就是每个状态都可以通过一步或者多步转移到达任意另一个状态。
- 正常返:可以理解为每个状态在有限步转移后再回到自己的概率为1。
如下图所示例子
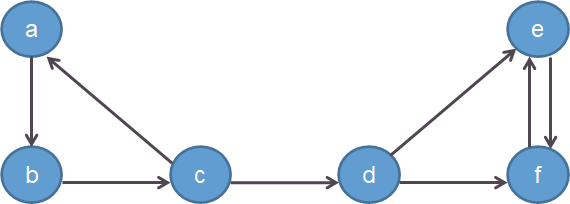
从图中可以看出,(a)可以通过(a
ightarrow b
ightarrow c
ightarrow d)到达(d),而(d)无法转移到(a)等状态,所以这个转移矩阵不可约。同理,当(a)转移到(d)等状态时,就再也无法回到(a),则该转移矩阵非正常返。这种情况下我们无法得到唯一的分布。
例如我们分别取初始分布为
状态转移矩阵为
则有
显然(x^infty_1
ot = x^infty_2)。
到这里我们说明了收敛性的问题,但其实真正在运用的时候还会遇到一些实际问题。下面,我们回到需要真正解决的AI模型排序的问题,用代码实现算法,并解决一些运用中遇到的实际问题。
三、实例分析
通过前述方式构建胜率矩阵,我们可以算得平稳分布,但还有一些实际问题需要微调算法。
对角线取值
在之前的网页排序里,对角线的元素被取为0,如果在胜率矩阵中也取为0,会出现错误的排序。假如胜率矩阵为
a b c
a 0 0.2 0.9
b 0.8 0 1
c 0.1 0 0
其中(a)对(b)的胜率为0.2,(a)对(c)的胜率为0.9;而(b)对(a)的胜率为0.8,(b)对(c)的胜率为1。可以很容易的看出(b)是最厉害的,(a)次之,(c)最弱。但如果我们直接套前面的计算方式,有
import numpy as np
T = np.matrix([[0 ,0.2,0.9],
[0.8, 0 , 1 ],
[0.1, 0 , 0 ]])
for i in range(T.shape[0]): # 归一化为状态转移概率矩阵
T[:,i] = T[:,i]/np.sum(T[:,i])
X = np.matrix([1/3,1/3,1/3]) # 初始分布
X = X.T
print(T)
print(T**2000*X)
得到
T:
[[0. 1. 0.47368421]
[0.88888889 0. 0.52631579]
[0.11111111 0. 0. ]]
X:
[[0.48579545]
[0.46022727]
[0.05397727]]
可以发现(a)居然比(b)的分值高,这显然是不合理的。出现这个问题的原因在于,在将胜率矩阵转化为概率矩阵时,归一化的操作改变了(b)指向(a)的权值,直接从0.2拉到了1,使得(b)把所有自身的重要度都贡献给了(a)。一个合理的解决办法是将对角线取为0.5,表示自己对自己的胜率是五五开。这种方式可以防止某个概率在归一化的过程中被不合理的放缩。此时胜率矩阵为:
a b c
a 0.5 0.2 0.9
b 0.8 0.5 1
c 0.1 0 0.5
计算得到
T:
[[0.35714286 0.28571429 0.375 ]
[0.57142857 0.71428571 0.41666667]
[0.07142857 0. 0.20833333]]
X:
[[0.31038506]
[0.66161027]
[0.02800467]]
可以看到,这个结果是合理的。同时这种方式还可以防止某一列出现全为0的情形。
构造不可约且正常返
通常我们需要考虑到各种胜负关系的情况,来保证平稳分布存在且唯一。假如胜率矩阵为
a b c
a 0.5 1 1
b 0 0.5 0.3
c 0 0.7 0.5
可以看出(a)对(b)和(c)的胜率都为1;而(c)对(b)的胜率为0.7。可以很容易的看出排序应该为(a,c,b)。但计算得到的结果为:
T:
[[1. 0.45454545 0.55555556]
[0. 0.22727273 0.16666667]
[0. 0.31818182 0.27777778]]
X:
[[1.]
[0.]
[0.]]
可以发现(b)和(c)的排序无法区分。出现这个问题的原因在于(a)是一个吸收态,只有指入没有指出。可以通过一个权值很小的均匀的转移矩阵进行微调。取
其中权重参数(alpha=0.001),则修正后的矩阵表示为(S = (1-alpha) imes T + alpha imes E)。这里的(T)是归一化为概率矩阵的(T)。此时有矩阵(S)对每个状态都至少有一个小的转移概率,即不存在吸收态。同时可以注意到(T)并不满足不可约且正常返的条件,但(T)存在平稳分布,这说明了之前的定理条件是充分条件,而非必要条件。可以留意一下这点。最终有
T = np.matrix([[0.5, 1 , 1 ],
[ 0 ,0.5,0.3],
[ 0 ,0.7,0.5]])
for i in range(T.shape[0]): # 归一化为状态转移概率矩阵
T[:,i] = T[:,i]/np.sum(T[:,i])
E = np.matrix(np.ones_like(T))/T.shape[0]
alpha = 1e-3
S = (1-alpha)*T+alpha*E
X = np.matrix([1/3,1/3,1/3]) # 初始分布
X = X.T
print(S)
print(S**2000*X)
得到
S:
[[9.99333333e-01 4.54424242e-01 5.55333333e-01]
[3.33333333e-04 2.27378788e-01 1.66833333e-01]
[3.33333333e-04 3.18196970e-01 2.77833333e-01]]
X:
[[9.98694573e-01]
[5.86177258e-04]
[7.19249506e-04]]
此结果合理,且可以看出(a)远远强于(c,b)。
完整代码及示例
最终代码封装为函数:
def pagerank(T):
assert type(T) == np.matrix, 'please use np.matrix'
for i in range(T.shape[0]):
T[:,i] = T[:,i]/np.sum(T[:,i])
E = np.matrix(np.ones_like(T))/T.shape[0]
alpha = 1e-3
S = (1-alpha)*T+alpha*E
X = np.matrix([1]*T.shape[0])/T.shape[0]
X = X.T
score = S**200*X
return score
我们给一个不太好肉眼判断的胜率关系如下:
a b c
a 0.5 0.6 0.3
b 0.4 0.5 0.6
c 0.7 0.4 0.5
这里三个模型出现了相互克制的情形,即
(a stackrel{beats}{longrightarrow} b stackrel{beats}{longrightarrow} c stackrel{beats}{longrightarrow} a),带入函数:
score:
matrix([[0.30789762],
[0.34109655],
[0.35100582]])
可得排序关系(c,b,a)。