初级模拟电路：3-9 BJT三极管实现逻辑门

回到目录

      BJT晶体管可以实现逻辑门，事实上，在场效应管被发明用于集成电路以前，各种逻辑门芯片中的电路就是用BJT晶体管来实现的。最早人们使用二极管与BJT组合来实现逻辑门，这个称为二极管-晶体管逻辑（Diode-Transistor Logic），简称DTL；后来改进为全部用BJT晶体管来实现逻辑门，这个称为晶体管-晶体管逻辑（Transistor-Transistor Logic），简称TTL。早期广为人知的TTL电平，就是基于这种用BJT晶体管实现的逻辑门。TTL的优点是响应速度比较快，缺点是功耗较大，所以后来基本被功耗更低的场效应管取代。

      我们这里仅介绍几个最简单的逻辑门的实现：反相器、或非门、与非门，主要是用来说明概念。除非你是专门设计逻辑门芯片的，否则一般平时也不太可能用分立元件去搭建逻辑门，还有就是在电路修补中万不得已时应急用一下。

      在前面几小节的放大电路中，BJT都工作于放大区。而在用BJT实现逻辑门时，却要使用饱和区和截止区，而不能使用放大区，这个是逻辑电路和放大电路的在使用BJT时的根本区别。

1. 反相器

      反相器的功能很简单，就是将输入的电平反向输出：输入高电平-输出低电平、输入低电平-输出高电平。下面是反相器的实现电路：

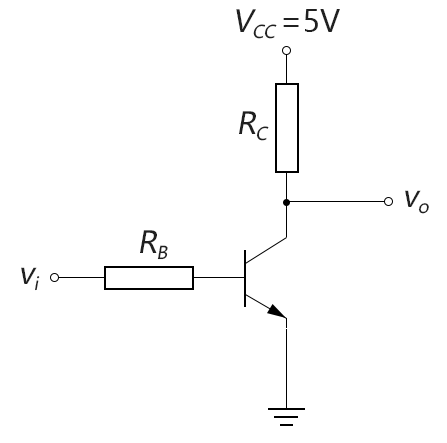
图3-9.01 

      在作逻辑分析时，我们一般做如下近似：将V_BE的导通值视为0.7V，将典型值为0.1V~0.3V的饱和电压V_CEsat近似视为0.2V。

      下面是反相器电路工作原理：

      • 当v_i输入为0V时，BJT截止，v_o输出电平即为5V。

      • 当v_o输入为5V时，BJT的CE端导通，产生电流I_C，若此时BJT处于饱和区，V_CE近似可视为饱和电压0.2V，此时输出电平v_o即为0.2V。

      这个电路的关键点在于如何选取合适的R_B与R_C值以确保BJT在导通时确实工作于饱和区。一般可以先根据外部负载条件定出一个符合输出阻抗要求的R_C，然后再根据饱和要求，用公式原理推算出能使BJT进入临界饱和的大致R_B值，再加点余量。最后验证在高电平输入条件下，BJT在此R_B配置下是否确实工作于饱和区。具体方法可参看下面的案例：

案例3-9-1：在下图的反相器中，已知β=100，根据外部负载匹配，要求R_C为500Ω，请选取合适的R_B值使反相器能正常工作。

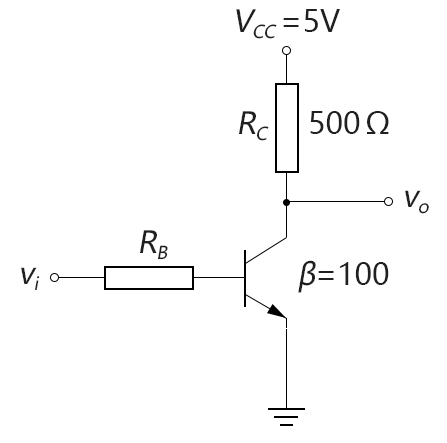
图3-09.a1 

解：先计算出，在这个R_C条件下，当BJT处于临界饱和时的I_Csat值：

      然后计算临界饱和时的I_Bsat值（当处于临界饱和时，β仍视为100）：

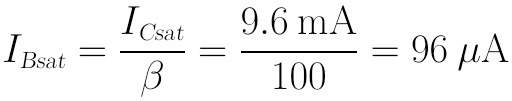
      使此I_Bsat成立的R_Bsat为：

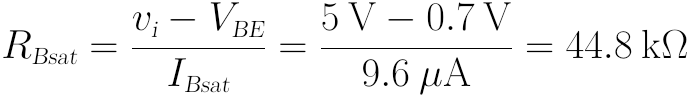
      为使BJT进入更深度的饱和，我们选取R_B为比R_Bsat更小的值，假定选取为20kΩ。

验证：当R_B为20kΩ时，I_B为：

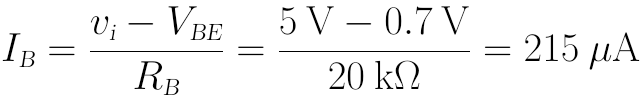
      此时电流放大倍数为：

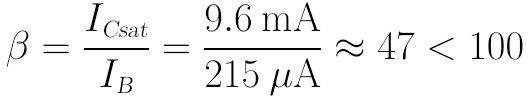
      可知，在此R_B值下，BJT导通时确实处于饱和区，原假设正确。

2. 或非门

      或非门BJT实现电路和输入输出真值表如下图所示（其中1表示高电平，0表示低电平）：

图3-9.02 

      • 当v_i1和v_i2输入都为0V时，晶体管Q₁和Q₂都截止，v_o输出电平为5V。

      • 当v_i1输入为5V、v_i2输入为0V时，晶体管Q₁导通、Q₂截止，由于Q₁工作于饱和区，V_CE1=V_CEsat≈0.2V，故v_o输出电平为0.2V。

      • 同样的，当v_i2输入为5V时、v_i1输入为0V时，晶体管Q₂导通、Q₁截止，V_CE2=V_CEsat≈0.2V，故v_o输出电平为0.2V。

      • 当v_i1和v_i2都输入0V时，晶体管Q₁和Q₂都导通，V_CE1=V_CE2=V_CEsat≈0.2V，故v_o输出电平为0.2V。

      关于如何配置R_B1、R_B2、R_C的值使BJT晶体管工作于饱和区，这个和前面反相器的计算方法是类似的，可参看上面的案例3-9-1。

3. 与非门

      与非门的实现需要二极管的配合，其实现电路和真值表如下图所示：

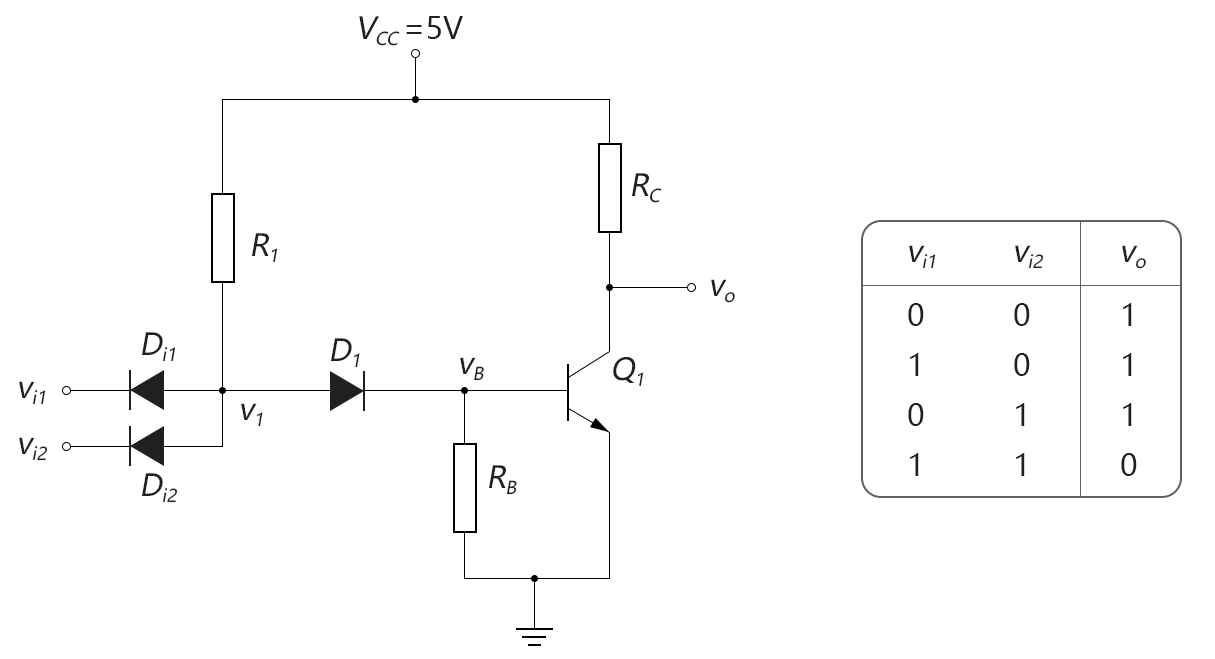
图3-9.03 

      • 当v_i1和v_i2输入中有任一个为0V时，输入二极管D_i1或D_i2就会导通，此时v₁点的电压即为二极管的导通阈值电压0.7V。这个电压无法使右边的D₁和Q₁都导通，因为若要使D₁和Q₁的发射结都导通，v_B点的电压起码需要0.7V，而v₁点的电压需要0.7+0.7=1.4V。而在v₁只有0.7V的情况下，右边的D₁和Q₁的发射结每个只能分到0.35V左右的电压，故D₁和Q₁都截止，输出v_o保持5V的高电平。

      • 当v_i1和v_i2输入全都为5V时，输入二极管D_i1和D_i2全都截止，此时V_CC会使R₁、D₁和Q₁形成通路，v_B点的电压为0.7V，v₁点的电压为1.4V。由于Q₁导通时工作于饱和状态，故输出v_o为V_CEsat约等于0.2V。

      至于如何配置R₁、R_B、R_C，原理和前面是一样的：根据输出阻抗匹配先定R_C，然后计算为使Q₁进入饱和区的R₁，具体方法可参看前面的案例3-9-1。

      顺便提一下，R_B称作下拉电阻，其主要作用是当Q₁从饱和状态切换到截止状态时，使基区过剩的少数载流子有个渠道流掉，以减少切换开关时间。这个稍微了解一下即可，一般选一个大约的几千欧的阻值就差不多了，在要求不高的场合下，即使不用R_B也问题不大。

4. 关于TTL

      在上面电路中，我们用DTL（二极管-晶体管逻辑）实现了与非门。如果你想知道传说中的TTL（晶体管-晶体管逻辑）到底是什么样的，那么本小节可以稍稍满足一下你的好奇心。

      我们仍以上面的与非门为例，假设先去掉D_i2，那么，在图中两个背靠背的二极管D_i1和D₁，其实可以看成是一个NPN型三极管，如下图所示：

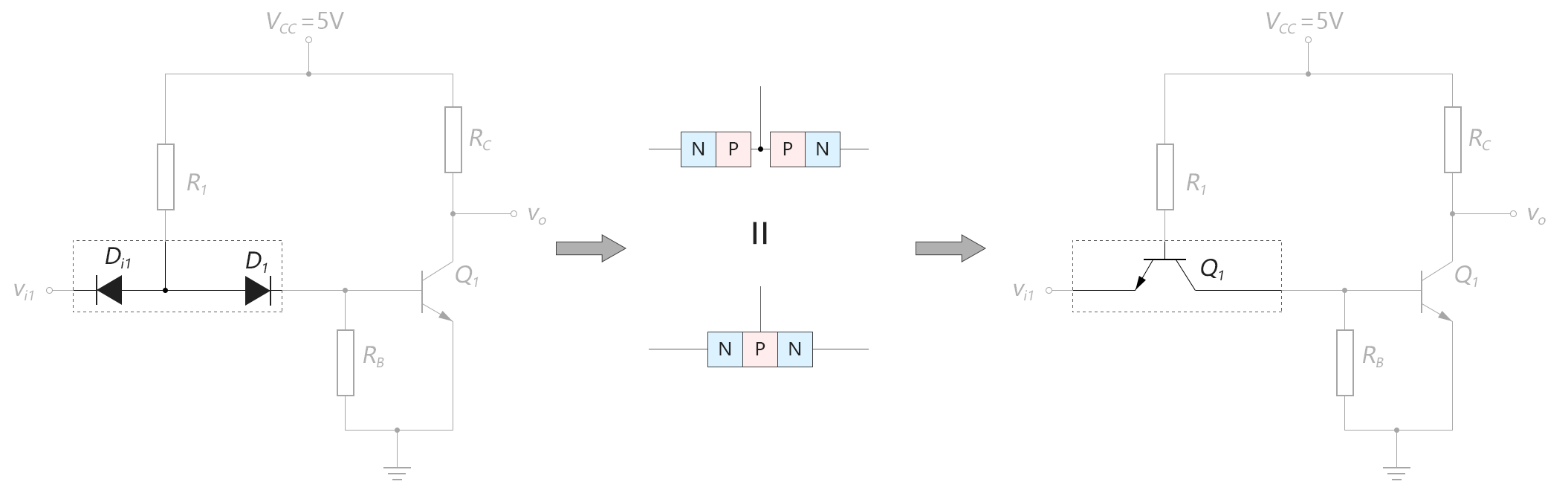
图3-9.04 

      我们前面说过，在分立元器件的BJT晶体管中，C极和E极的掺杂浓度是不对称的，所以分立元器件中不能像上图这样等效，但是在制作集成电路芯片时，是可以在片上做成像上面右图那样的对称管的。

      而且，在集成电路制作时还可以加入多个发射极，如下图所示：

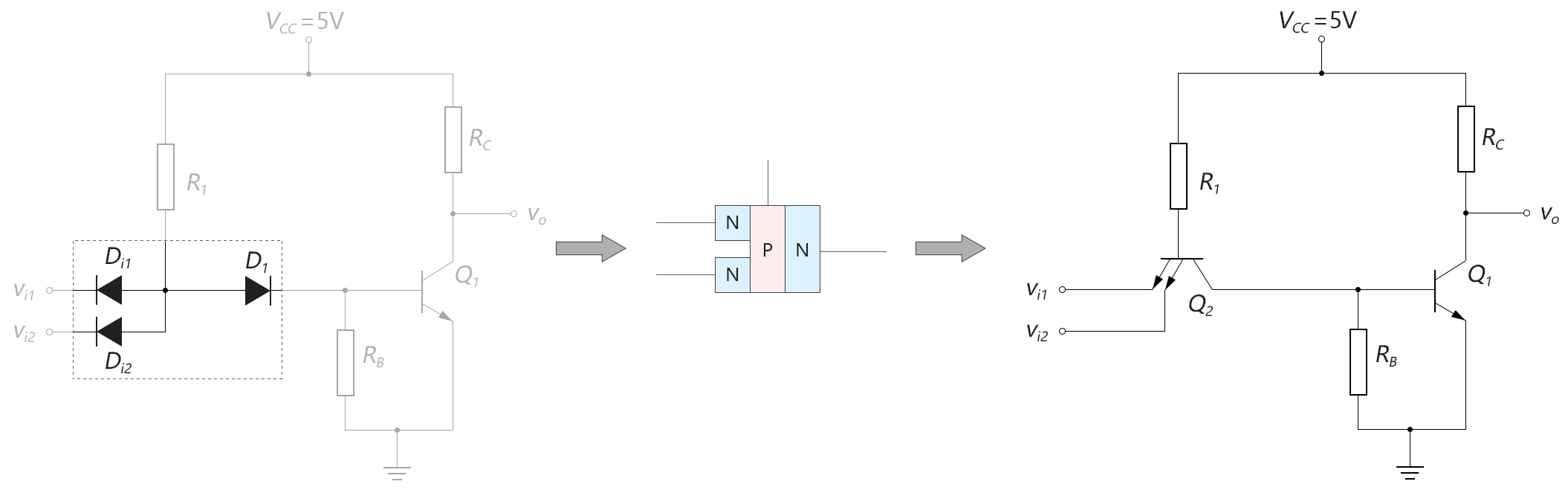
图3-9.05 

      如此，就实现了一个二输入与非门的TTL电路。如果要实现n个输入的与非门，还可以加入n多个发射极。当然，这种多发射极的BJT晶体管只能在集成电路芯片中实现，分立元器件的话是没有这种器件的。

     

回到目录

（ end of 3-9）

---