题目大意:
现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到,但抓兔子还是比较在行的,
而且现在的兔子还比较笨,它们只有两个窝,现在你做为狼王,面对下面这样一个网格的地形:

左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路
1:(x,y)<==>(x+1,y)
2:(x,y)<==>(x,y+1)
3:(x,y)<==>(x+1,y+1)
道路上的权值表示这条路上最多能够通过的兔子数,道路是无向的. 左上角和右下角为兔子的两个窝,
开始时所有的兔子都聚集在左上角(1,1)的窝里,现在它们要跑到右下解(N,M)的窝中去,狼王开始伏击
这些兔子.当然为了保险起见,如果一条道路上最多通过的兔子数为K,狼王需要安排同样数量的K只狼,
才能完全封锁这条道路,你需要帮助狼王安排一个伏击方案,使得在将兔子一网打尽的前提下,参与的
狼的数量要最小。因为狼还要去找喜羊羊麻烦.
Input
第一行为N,M.表示网格的大小,N,M均小于等于1000.
接下来分三部分
第一部分共N行,每行M-1个数,表示横向道路的权值.
第二部分共N-1行,每行M个数,表示纵向道路的权值.
第三部分共N-1行,每行M-1个数,表示斜向道路的权值.
输入文件保证不超过10M
Output
输出一个整数,表示参与伏击的狼的最小数量.
Sample Input
3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6
Sample Output
14
基本思路:
据说Dicnic会被卡,据说剪枝一下就过了,蒟蒻表示根本不理解dicnic,
所以还是想直接上更快的sap算法,虽然理解的也不是恨透,但今天来不及了,明天再提交一次;
所以还是最小割转对偶图最短路,详见周冬的论文<<浅析最大最小定理在信息学竞赛中的应用>>
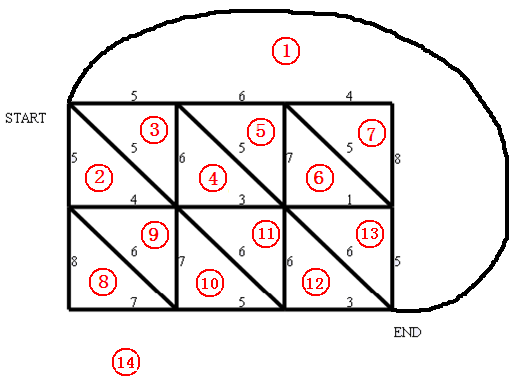
对偶图就是在原图中标号,然后找规律构造,如上图(借用了其他人的图);
我不知道如果不是这种规则的图,还能不能构造出对偶图,个人觉得不行;
这样堆优化的dijkstra的时间复杂度就是O(nlogn)
代码如下:
#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<string>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
typedef long long ll;
typedef long long LL;
typedef pair<int,int> pii;
const int inf = 0x3f3f3f3f;
const int maxn = 1000000;
const ll mod = 1e9+9;
int n,m,num,cnt;
struct Edge{
int v,w,next;
}edge[6*maxn+100];
int head[2*maxn+100],dis[2*maxn+100];
bool vis[2*maxn+100];
struct Node{
int v,w;
Node(int _v,int _w):v(_v),w(_w) {}
bool operator<(const Node& a)const{
return w>a.w;
}
};
void addEdge(int u,int v,int w){
edge[cnt].v=v;
edge[cnt].w=w;
edge[cnt].next=head[u];
head[u]=cnt++;
}
void dijkstra(int s){
memset(vis,false,sizeof(vis));
memset(dis,inf,sizeof(dis));
dis[s]=0;
Node tmp(s,0);
priority_queue<Node>pq;
pq.push(tmp);
while(!pq.empty()){
tmp=pq.top();
pq.pop();
int u=tmp.v;
if(vis[u]){
continue;
}
vis[u]=true;
for(int i=head[u];i!=-1;i=edge[i].next){
int v=edge[i].v;
int w=edge[i].w;
if(dis[v]>dis[u]+w){
dis[v]=dis[u]+w;
pq.push(Node(v,dis[v]));
}
}
}
}
int main(){
scanf("%d%d",&n,&m);
if(n==1||m==1){
int ans=inf;
int _max=max(n,m);
for(int i=1;i<_max;i++){
int u;
scanf("%d",&u);
ans=min(ans,u);
}
printf("%d
",ans);
return 0;
}
cnt=0;
memset(head,-1,sizeof(head));
int u,v,w;
for(int i=1;i<=n;i++){
for(int j=1;j<m;j++){
scanf("%d",&w);
if(i==1){
u=1;
v=j*2+1;
addEdge(u,v,w);
addEdge(v,u,w);
}else if(i==n){
u=(n-1)*(m-1)*2+2;
v=((i-2)*(m-1)+j)*2;
addEdge(u,v,w);
addEdge(v,u,w);
}else{
u=((i-2)*(m-1)+j)*2;
v=((i-1)*(m-1)+j)*2+1;
addEdge(u,v,w);
addEdge(v,u,w);
}
}
}
for(int i=1;i<n;i++){
for(int j=1;j<=m;j++){
scanf("%d",&w);
if(j==1){
u=(n-1)*(m-1)*2+2;
v=((i-1)*(m-1)+j)*2;
addEdge(u,v,w);
addEdge(v,u,w);
}else if(j==m){
u=1;
v=((i-1)*(m-1)+j-1)*2+1;
addEdge(u,v,w);
addEdge(v,u,w);
}else{
u=((i-1)*(m-1)+j-1)*2+1;
v=((i-1)*(m-1)+j)*2;
addEdge(u,v,w);
addEdge(v,u,w);
}
}
}
for(int i=1;i<n;i++){
for(int j=1;j<m;j++){
scanf("%d",&w);
u=((i-1)*(m-1)+j)*2;
v=((i-1)*(m-1)+j)*2+1;
addEdge(u,v,w);
addEdge(v,u,w);
}
}
num=(n-1)*(m-1)*2+2;
dijkstra(1);
printf("%d
",dis[num]);
return 0;
}