CF-Mr. Kitayuta's Colorful Graph

B. Mr. Kitayuta's Colorful Graph

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Mr. Kitayuta has just bought an undirected graph consisting of n vertices and m edges. The vertices of the graph are numbered from 1 to n. Each edge, namely edge i, has a color c_i, connecting vertex a_i and b_i.

Mr. Kitayuta wants you to process the following q queries.

In the i-th query, he gives you two integers — u_i and v_i.

Find the number of the colors that satisfy the following condition: the edges of that color connect vertex u_i and vertex v_i directly or indirectly.

Input

The first line of the input contains space-separated two integers — n and m (2 ≤ n ≤ 100, 1 ≤ m ≤ 100), denoting the number of the vertices and the number of the edges, respectively.

The next m lines contain space-separated three integers — a_i, b_i (1 ≤ a_i < b_i ≤ n) and c_i (1 ≤ c_i ≤ m). Note that there can be multiple edges between two vertices. However, there are no multiple edges of the same color between two vertices, that is, if i ≠ j, (a_i, b_i, c_i) ≠ (a_j, b_j, c_j).

The next line contains a integer — q (1 ≤ q ≤ 100), denoting the number of the queries.

Then follows q lines, containing space-separated two integers — u_i and v_i (1 ≤ u_i, v_i ≤ n). It is guaranteed that u_i ≠ v_i.

Output

For each query, print the answer in a separate line.

Sample test(s)

Input

4 5
1 2 1
1 2 2
2 3 1
2 3 3
2 4 3
3
1 2
3 4
1 4

Output

2
1
0

Input

5 7
1 5 1
2 5 1
3 5 1
4 5 1
1 2 2
2 3 2
3 4 2
5
1 5
5 1
2 5
1 5
1 4

Output

1
1
1
1
2

Note

Let's consider the first sample.

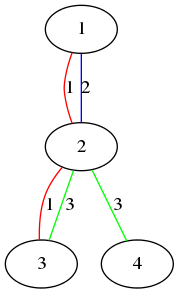The figure above shows the first sample.

• Vertex 1 and vertex 2 are connected by color 1 and 2.
• Vertex 3 and vertex 4 are connected by color 3.
• Vertex 1 and vertex 4 are not connected by any single color.

---

思路：

很不错的一道题目。

首先看他最后的那个问题“Find the number of the colors that satisfy the following condition: the edges of that color connect vertex u_i and vertex v_i directly or indirectly.”找出可以连通两点的个数，那个可以把这个问题退一步——相同颜色的点怎样才算是连通？

其实这就是一道更高维度的并查集，从而更好的揭示了并查集的实质：两个点的连通问题——他们连通的条件是什么？

这道题是对这一隐藏现象的揭示

---

#include <iostream>
#include <cstring>
#include <cstdio>
#define maxn 207
using namespace std;

int set[maxn][maxn];

int init()
{
    for(int i = 1;i <= maxn;i++)
        for(int j = 1;j <= maxn;j++)
            set[i][j] = j;
}

int find(int color,int x)
{
    int i;
    for(i = x;i != set[color][i];i = set[color][i])
        set[color][i] = set[color][set[color][i]];
    return i;
}

void set_together(int color,int t1,int t2)
{
    int fx = find(color,t1);
    int fy = find(color,t2);
    if(fx != fy)
        set[color][fx] = fy;
}

int main()
{
    int q;
    int n,m;
    int t1,t2,t;
    int ans;
    while(~scanf("%d%d",&n,&m))
    {
        init();
        for(int i = 1;i <= m;i++)
        {
            scanf("%d%d%d",&t1,&t2,&t);
            set_together(t,t1,t2);
        }
        scanf("%d",&q);
        while(q--)
        {
            ans = 0;
            scanf("%d%d",&t1,&t2);
            for(int i = 1;i <= m;i++)
                if(find(i,t1) == find(i,t2)) ans++;
            cout<<ans<<endl;
        }
    }
    return 0;
}