不能重复:
[抄题]:
给出一个候选数字的set(C)和目标数字(T),找到C中所有的组合,使找出的数字和为T。C中的数字可以无限制重复被选取。
例如,给出候选数组[2,3,6,7]和目标数字7,所求的解为:
[7],
[2,2,3]
[思维问题]:
- 以为要在dfs函数中不断添加,其实用的是two sum的思想:反向寻找sum - nums[i]
- 为了避免重复取数,需要先排序去重
[一句话思路]:
[输入量]:空: 正常情况:特大:特小:程序里处理到的特殊情况:异常情况(不合法不合理的输入):
[画图]:
[一刷]:
- index和前面数不同时才+1,因此新数组容量需要+1
- 如果remainTarget比nums[i]小,直接break,退出所有循环
[二刷]:
- 数组要先排序,再去重
- DFS中应该先是返回条件,再是循环中的循环退出条件。循环中的参数是i,不是startIndex,startIndex是所有数组的开头
- combinations.add(nums[i]);添加的是数组中的元素,不是角标,毕竟是对元素进行处理
[三刷]:
[四刷]:
[五刷]:
[五分钟肉眼debug的结果]:
[总结]:
helper函数反复选i
[复杂度]:Time complexity: O() Space complexity: O()
[英文数据结构或算法,为什么不用别的数据结构或算法]:
[其他解法]:
[Follow Up]:
[LC给出的题目变变变]:
[代码风格] :

public class Solution { /** * @param candidates: A list of integers * @param target:An integer * @return: A list of lists of integers */ public List<List<Integer>> combinationSum(int[] candidates, int target) { List<List<Integer>> results = new ArrayList<>(); if (candidates == null || candidates.length == 0) { return results; } int[] nums = removeDuplicates(candidates); dfs(nums, 0, new ArrayList<Integer>(), target, results); return results; } private int[] removeDuplicates(int[] candidates) { Arrays.sort(candidates); int index = 0; for (int i = 0; i < candidates.length; i++) { if (candidates[i] != candidates[index]) { candidates[++index] = candidates[i]; } } int[] nums = new int[index + 1]; for (int i = 0; i < index + 1; i++) { nums[i] = candidates[i]; } return nums; } private void dfs(int[] nums, int startIndex, List<Integer> combination, int remainTarget, List<List<Integer>> results) { if (remainTarget == 0) { results.add(new ArrayList<Integer>(combination)); return; } for (int i = startIndex; i < nums.length; i++) { if (remainTarget < nums[i]) { break; } combination.add(nums[i]); dfs(nums, i, combination, remainTarget - nums[i], results); combination.remove(combination.size() - 1); } } }
能重复:
[抄题]:
[思维问题]:
知道:不用remove duplicate函数。先排序,helper函数中改成i+1
结果:
[7,1,2,5,1,6,10] 8
输出[[1,1,6],[1,2,5],[1,7],[1,2,5],[1,7],[2,6]]
期望[[1,1,6],[1,2,5],[1,7],[2,6]]问题:不知道怎么结果去重
[一句话思路]:
[输入量]:空: 正常情况:特大:特小:程序里处理到的特殊情况:异常情况(不合法不合理的输入):
[画图]:
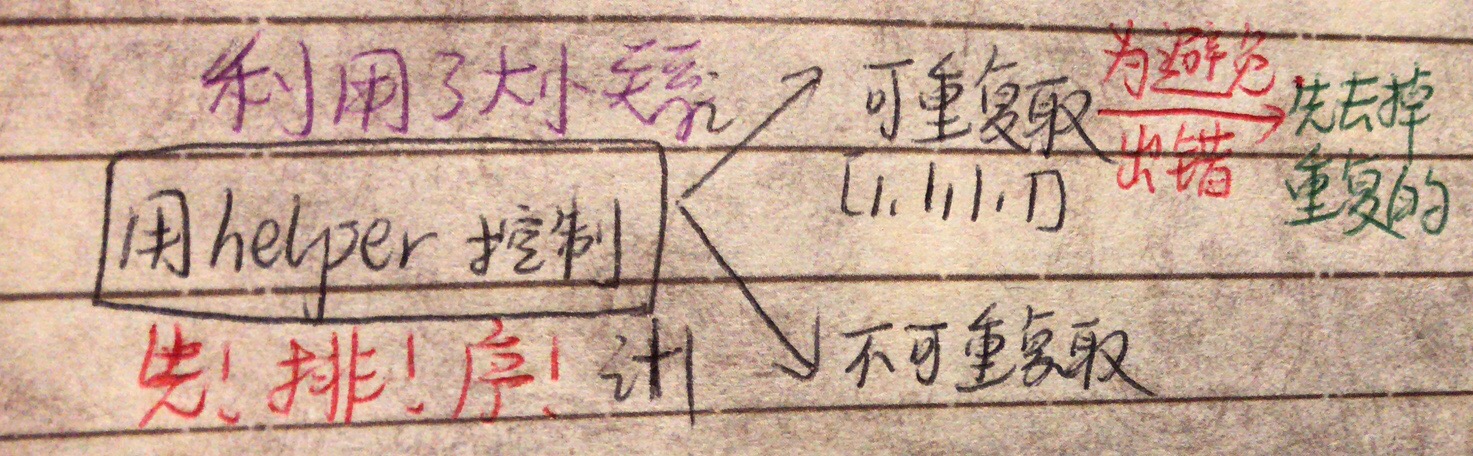
[一刷]:
[二刷]:
[三刷]:
[四刷]:
[五刷]:
[五分钟肉眼debug的结果]:
[总结]:
[复杂度]:Time complexity: O() Space complexity: O()
[英文数据结构或算法,为什么不用别的数据结构或算法]:
[其他解法]:
[Follow Up]:
[LC给出的题目变变变]:
[代码风格] :

public class Solution { /** * @param num: Given the candidate numbers * @param target: Given the target number * @return: All the combinations that sum to target */ public List<List<Integer>> combinationSum2(int[] candidates, int target) { List<List<Integer>> results = new ArrayList<>(); if (candidates == null || candidates.length == 0) { return results; } Arrays.sort(candidates); List<Integer> combination = new ArrayList<Integer>(); helper(candidates, 0, combination, target, results); return results; } private void helper(int[] candidates, int startIndex, List<Integer> combination, int target, List<List<Integer>> results) { if (target == 0) { results.add(new ArrayList<Integer>(combination)); return; } for (int i = startIndex; i < candidates.length; i++) { if (i != startIndex && candidates[i] == candidates[i - 1]) { continue; } if (target < candidates[i]) { break; } combination.add(candidates[i]); helper(candidates, i + 1, combination, target - candidates[i], results); combination.remove(combination.size() - 1); } } }
