前面的博客有介绍过对连续的变量进行线性回归分析,从而达到对因变量的预测或者解释作用。那么如果因变量是离散变量呢?在做行为预测的时候通常只有“做”与“不做的区别”、“0”与“1”的区别,这是我们就要用到logistic分析(逻辑回归分析,非线性模型)。
参数解释(对变量的评价)
发生比(odds): ODDS=事件发生概率/事件不发生的概率=P/(1-P)
发生比率(odds ratio):odds ratio=oddsB/oddsA (组B相对于组A更容易发生的比率)
注:odds ratio大于1或者小于1都有意义,代表自变量的两个分组有差异性,对因变量的发生概率有作用。若等于1的话,该组变量对事件发生概率没有任何作用。
参数估计方法
线性回归中,主要是采用最小二乘法进行参数估计,使其残差平方和最小。同时在线性回归中最大似然估计和最小二乘发估计结果是一致的,但不同的是极大似然法可以用于非线性模型,又因为逻辑回归是非线性模型,所以逻辑回归最常用的估计方法是极大似然法。
极大似然公式:L(Θ)=P(Y1)P(Y2)...p(YN) P为事件发生概率PI=1/(1+E-(α+βXI))
在样本较大时,极大似然估计满足相合性、渐进有效性、渐进正太性。但是在样本观测少于100时,估计的风险会比较大,大于100可以介绍大于500则更加充分。
模型评价
这里介绍拟合优度的评价的两个标准:AIC准则和SC准则,两统计量越小说明模型拟合的越好,越可信。
若事件发生的观测有n条,时间不发生的观测有M条,则称该数据有n*m个观测数据对,
在一个观测数据对中,P>1-P,则为和谐对(concordant)。P<1-P,则为不和谐对(discordant)。P=1-P,则称为结。
在预测准确性有一个统计量C=(NC-0.5ND+0.5T)/T,其中NC为和谐对数,ND为不和谐对数,这里我们就可以根据C统计量来表明模型的区分度,例如C=0.68,则表示事件发生的概率比不发生的概率大的可能性为0.68。
使用假设条件
①数据来自随机样本
②共线性敏感,自变量之间是非线性关系
③因变量只能取0、1
接下来看案例
PROC LOGISTIC DATA=EX.LOAN PLOTS(ONLY)=(EFFECT(CLBAND X=(DELINQ DEBTINC REASON)) ODDSRATIO (TYPE=HORIZONTALSTAT RANGE=CLIP)); CLASS EDUCATION(REF="college") REASON(REF="car")/PARAM=REFERENCE; MODEL BAD(EVENT="1")=DELINQ DEBTINC YROPEN EDUCATION REASON DELINQ*DEBTINC DEBTINC*EDUCATION/CLODDS=PL STB PARMLABEL; UNITS DEBTINC=5 -5; ODDSRATIO EDUCATION/DIFF=ALL CL=PL; ODDSRATIO REASON/DIFF=ALL CL=PL; TITLE "BAD LOAN MODEL"; RUN;
PROC LOGISTIC可以用的常见的选项是noprint 、plots、namelen=n 分别对应功能为:不打印结果、输出画图、变量名长度为N(20~200)。其中plots语句中有ONLY表明指输出接下来指定图形。
后面跟着个effect选项,括号中的自选项有CLBAND和showobs指定在图形中表明预测概率的置信区域和观测,后面还有子选项X=变量1 变量2.....表明画出多个自变量的预测效应图(假设其余变量都取均值,只考虑指定自变量的因变量预测情况)。这里指定了三个变量,就会输出三个预测效果图。注:因变量分类大于2则effect失效。
PROC LOGISTIC的选项ODDSRATIO,后面跟着两个子选项TYPE和range,type=horizontalstat表明图形有段显示发生比率和置信区间,range=clip表明图形横坐标的范围是计算到的最小发生比率到最大发生比率。
语句CLASS,选项PARAM=可以去三个值:EFFECT REFERENCEORDINAL,分别对应了三种不同将一个自变量分解成K-1个新变量的不同取值方法(一个变量有K个水平第 k个水平为参考水平!)三种方法的不同在于对参考水平变量取值分别去-1、0、按水平的升序取值(用于顺序变量)。
选项REF=‘’的作用为指定变量中的某个取值作为参考水平。
MODEL语句有且只能有一个。这里的因变量BAD后面跟着选项event=“1”表明bad值为1时代表事件发生,此模型是计算BAD=1发生的概率。然后等号后面跟着可能进入模型的自变量,其中还有两个交互的自变量,为了研究两个变量是否有交互作用。
model 后面跟着选项CLODDS=表示输出事件发生比率的执行区间(PL表示用剖面函数计算, wald表示根据wald检验计算,both表示两种方法都计算一遍)。
model后面的选项STB表示对输出标准化,此选项是针对不同变量的度量单位可能不一致作用的,标准化后能更加客观的对比不同变量对预测因变量的作用的大小。
model后面还有选项parmlabel表明为极大似然估计的表中输出标签。
UNITS语句:上代码中表示DEBTINNC的值增加或者减少5个单位时计算一次发生比率。(默认变化一个单位计算一次,变化非常微小,步长跨度大一些会更有意义)。
ODSSRATIO语句,计算某一自变量的水平相对于参考水平的发生比率,选项DIFF=ALL表示比较所有水平间的发生比率,DIFF=REF表明相对参考水平的发生比率。选项CL=WALDPLBOTH和上文中讲的一致。
一下是输出结果:
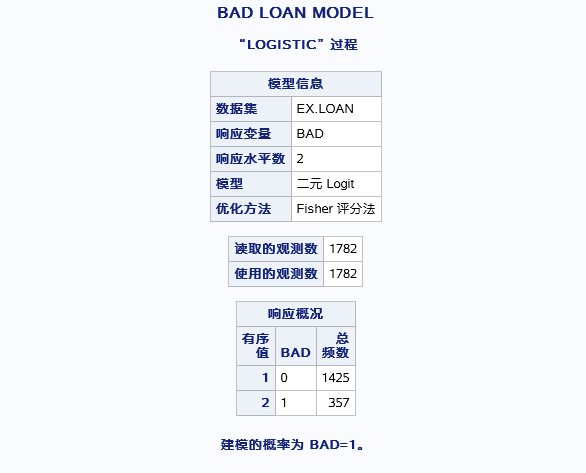
先输出一些基本情况,因变量水平数,观测数,以及频数,重要的是以什么条件建模(BAD=1)
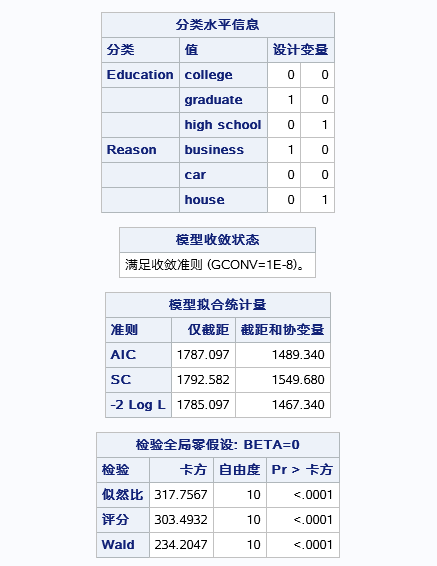
表一为根据两个变量的取不同水平,创建的新变量的取值
表二为模型的拟合优度判断,几个统计量是用于同一数据不同模型之间的比较才有意义,这里可以暂时忽略。
表三原假设为无线性关系(全局0假设),而根据三个统计量判断均是拒绝原假设,表示logit于自变量的线性关系显著。
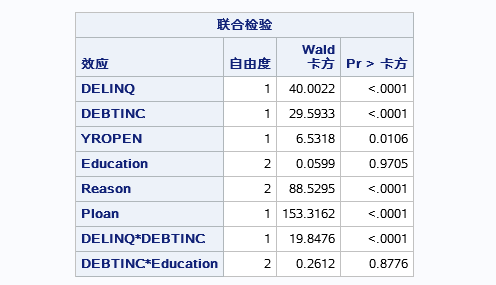
上表为变量的联合检验,也成为三效应检验,分别表示各个自变量对模型的显著性,即对因变量事件的发生有没有显著性。
以0.05的置信水平上有EDUCATION和DEBTINC*EDUCAION变量对模型没有显著性,其余的都有显著性。
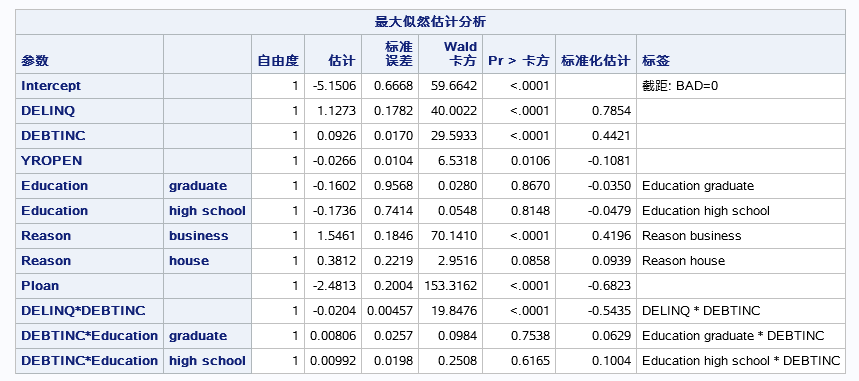
各个变量的参数估计包括截距的估计,还有标准化的参数估计(因为用了STB选项)。标准化后的估计值一般用来衡量不同自变量对因变量影响的大小(仅限于连续自变量,对于分类自变量标准化参数估计无意义)。还有一个统计量用于检查参数非零的显著性。
需要注意的是这里有两个变量EDUCATION和REASON的不同水平单独作为了一个变量进入模型。
注:以上是对所有变量都进行的参数估计,若在model后面再加一个选项SELECTION=FORWARDBCKWARDSTEPWISESCORE指明一个模型选择法,则最终的结果就想之前的博客中一样,一步一步选择变量,最终得到一个类似于上表的表,区别在于不能进如模型的变量会不存在表中,如下图是向前选择的最终结果:
(一下为插入别的代码结果)
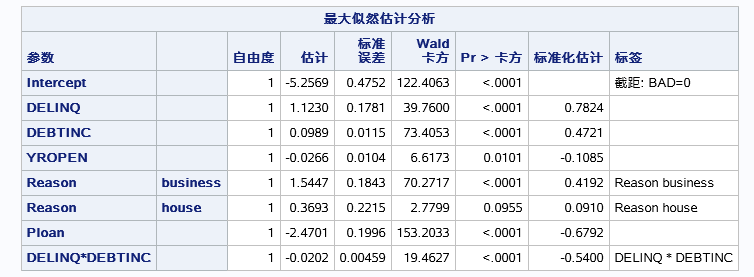
可见对变量进行筛选之后和不筛选是有区别的,一般认为筛选过的模型更加准确。
(以上为插入)
(以下为接着插入前的结果分析)
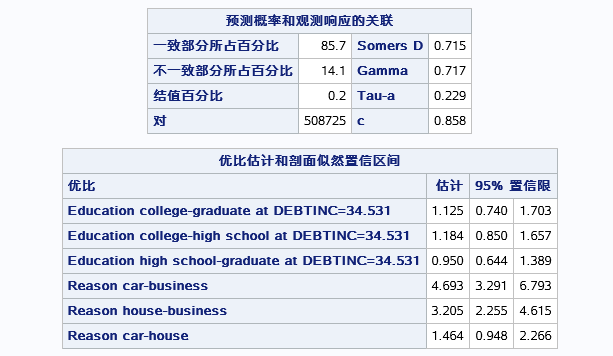
表一能衡量预测的准确性,一致部分的百分比即和观测于预测相同的占比有85.7,不一致的有14.1,不能确定的有0.2.。比较有价值的统计量是发生比率C=0.858,表明事件发生的概率比事件不发生的概率大的可能性有0.858。证明模型的有效。
表二,由于程序用了oddsratio语句,最用对象为EDUCATION和REASON,系统对两个变量的不同水平进行了求发生比率估计,即表二。前文说了发生比率不能等于1,而其中有两个新变量的置信区间包含了1,说明不同水平间对于发生比是无差别的,即新变量对发生不显著的。所以该模型中只有REASON 中BUSINESS和car两个水平的发生比是显著的,还有一个reason中house和business两水平的发生比是显著的。
还可以从图中看出相同结果:

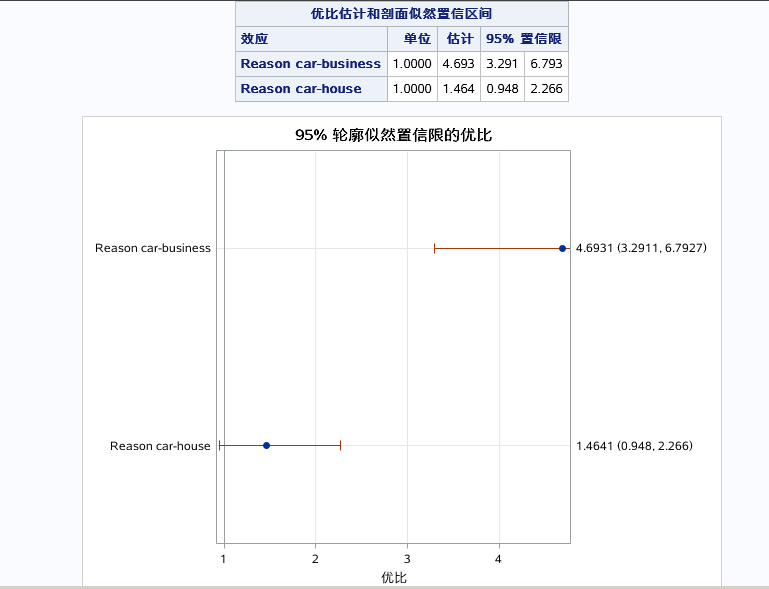
跟之前同理。

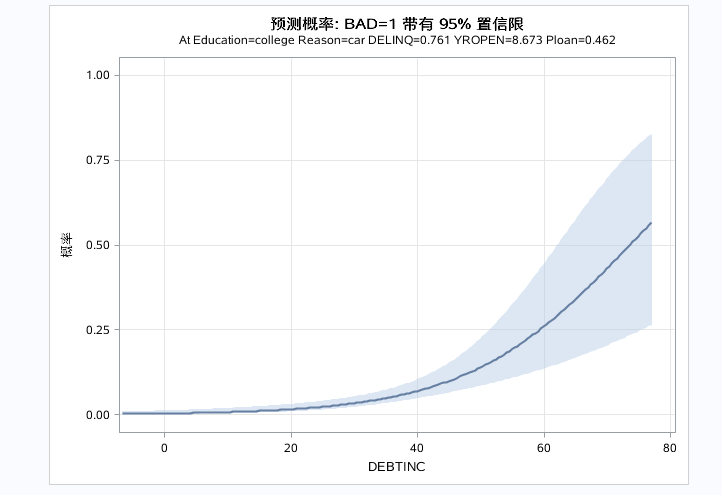
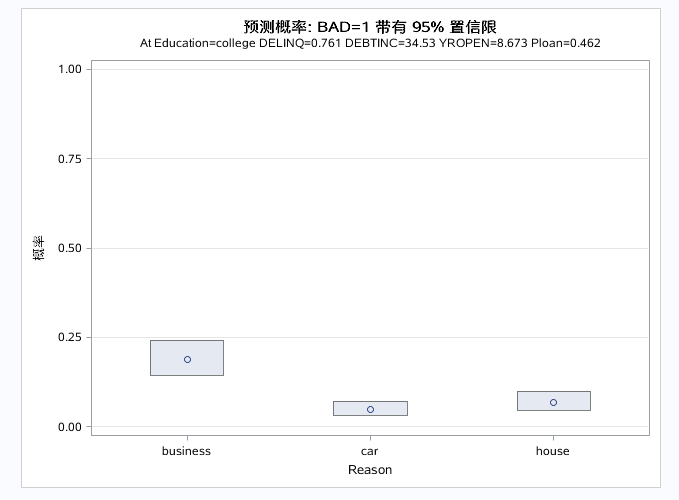
以上三图为自变量的预测效应图,分别控制别的自变量为均值或者参考水平是,单独看指定自变量和对因变量的预测效果。DEBTINC取值越大,预测概率越大。DELINQ取值越大,预测概率越大。对于分类变量得出business的预测概率最大。