判别分析

实际意义

判别分析于聚类分析的功能差不多，区别在于，聚类分析之前，没有人知道具体的是怎么分的类，分了哪几大类。而判别分析是已经把类别给分好，要做的是把没有分好类的数据观测，按照之前分好的类再进行分类。这里不同于生活中常见的分类先有具体的分类逻辑（这里叫做判别函数）。所以判别分的难点在于先由分好类的数据观测找到一个或者多个判别函数，然后对未进行分类的观测按照该判别公式进行分类。

进行判别分析需要满足的条件是：

①每一个判别变量都不能是其他判别变量的线性组合

②各个判别变量之间具有多元正态分布，即控制N-1个变量为固定值时，第N个变量满足正态分布

③满足②条件时，使用参数法计算判别函数，否则使用非参数法计算判别函数。

判别分析方法

距离判别法：D²(X)=(X-μ)²/σ²

马氏距离（广义平方距离）：W(X)=D_B²(X)-D_A²(X)

BAYES判别法：有先验概率，再有后验概率，最后还有错判概率

FISHER判别法：投影法

判别分析的实现

PROC DISCRIM、PROC CANDISC 、PROC STEPDISC过程步实现

PROC DISCRIM可以处理满足多元正态分布，也可以不满足该条件都可以处理。若满足多元正态分布，则可以计算出一次或者二次的判别函数（在组间方差不相等的情况下）。

PROC CANDISC是专门进行典型判别分析的过程，基于分析数值变量（类似于主成分分析结果）。能计算出最能描述组间差异的典型变量，然后结果仅给出典型变量和得分数据，后续要由PROC DISCRIM完成。

PROC STEPDISC逐步判别分析。最有效的找出体现不同类别的变量。

DATA CARS_TYPES CARS_TEST;
    SET SASHELP.CARS;
    BY MAKE TYPE;
    WHERE TYPE IN("SUV","Sedan","Sports");
    IF FIRST.TYPE THEN DO;
        IF ORIGIN IN ("USA","Europe")
        THEN OUTPUT CARS_TYPES;
        ELSE OUTPUT CARS_TEST;
    END;
RUN;
PROC DISCRIM DATA=CARS_TYPES TESTDATA=CARS_TEST METHOD=NORMAL
                POOL=TEST DISTANCE LIST TESTOUT=CARS_RESULT;
    CLASS TYPE;
    VAR WEIGHT WHEELBASE LENGTH MPG_CITY ENGINESIZE;
RUN;

分析的数据集是CARS_TYPES,即是根据此数据集的分类结果找到判别函数（可能是一次函数，也可能是二次函数），然后用从待分类的数据集，的观测用该判别函数进行分类，进而得出结果。(分析数据集和带分析数据集可以是一个数据集也可以是两个数据集，一个数据集则要求待分类的观测在type变量为缺失，两个数据集则要求变量名完全一致。)

METHOD=NORMAL，说明指定用参数法，若要指明用非参数法则用NPAR。该选项默认值为NORMAL。

POOL=TEST,指明使用假设检验来判断不同类间的协方差矩阵是否齐性。还可以是YES(使用合并后的协方差矩阵进行计算)、还可以是NO(使用不同类各自的协方差矩阵进行计算)。

DISTANCES输出不同类间的距离。

LIST输出后验概率。

接下来看结果：

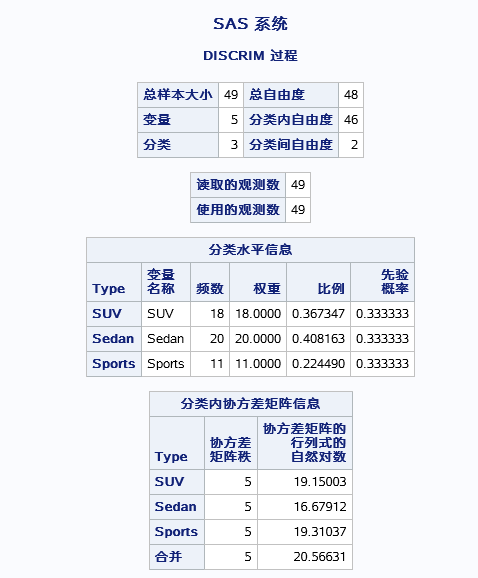
先是描述行统计结果，然后是不同类间的先验概率表，然后是不同类的协方差矩阵秩（非零特征值个数）和行列式自然对数，是用来自然对数是用来构造判别函数的。

判定不同类间的协方差矩阵是否齐性，由图可知，拒接原假设，所以协方差矩阵不完全相同。

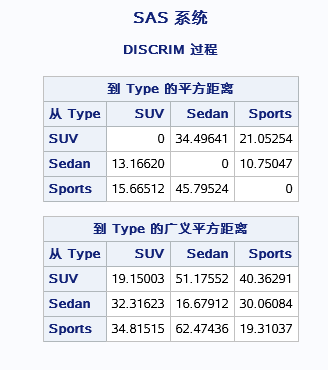
各自的距离。除了用来看区别效果之外，还可以用来生成判别函数。

LIST选项输出的后验概率，

对于分析数据集，判别函数的后验情况以及错判概率。

对于待分类数据集，分析函数的后验情况以及错判情况。

最终CARS_TEST的分类情况有_INTO_字段展现。

PROC CANDISC，主要思想是：用主成分分析找出若干个原始变量的线性组合，这些线性组合能解释绝大部分组间差异。

DATA CARS_TEST_NOTYPE;
    SET CARS_TEST;
    TYPE=" ";
RUN;
PROC SQL;
    CREATE TABLE CARS_ALL AS
    SELECT * FROM CARS_TYPES
    UNION
    SELECT * FROM CARS_TEST_NOTYPE;
QUIT;
PROC CANDISC DATA=CARS_ALL OUT=CARS_ALL_RESULTS DISTANCE;
    CLASS TYPE;
    VAR WEIGHT WHEELBASE LENGTH MPG_CITY ENGINESIZE;
RUN;

结果如下：

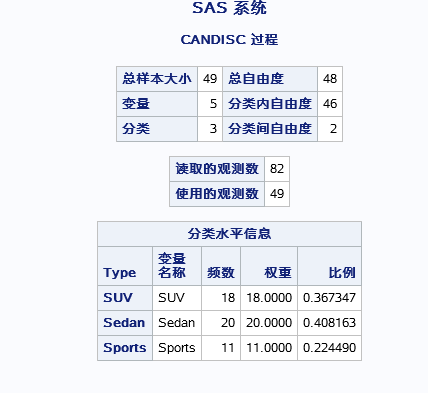
以上和PROC DISCRIM结果类似，不解释。

用了四种检验方法来检验各分类均值齐性。结果是怎么就看均值都不完全相等。

先看前半部分典型相关变量的统计结果（两个典型相关系数的取值），中间是两个典型相关系数can1和can2的特征值即累积解释贡献率，最后部分是检验典型相关是否为0，结果是典型相关不为0，两者之间有线性相关关系。

给出了三种判别系数。

 

最后给出不同类观测在典型变量can1和can2上的均值。

 然后再用PROC DISCRIM进行type的划分：

PROC DISCRIM DATA=CARS_ALL_RESULTS METHOD=NORMAL POOL=TEST
                OUT=CARS_RESULTS2;
    CLASS TYPE;
    VAR CAN1 CAN2;
RUN;

最后结果：

PROC STEPDISC逐步判别分析分为：向前选择（FORWARD）、向后选择（BACKWARD）、逐步选择（STEPWISE）。

逐步选择可以看作是向前和向后选择的结合。在最开始模型中不包含任何变量。然后在模型中添加判别能力最强的变量（R²越接近1），随着模型中变量的添加，先前引入的变量怕别能力可能有所变化，可以把低于阈值的变量从模型中删除。反复引入删除的过程，知道模型中变量都满足WILKS'S LAMBDA相似准则，并且其他变量都达不到为止。（不能再删，也不能再添加。）

PROC STEPDISC METHOD=STEPWISE DATA=CARS_ALL;
    CLASS TYPE;
    VAR WEIGHT WHEELBASE LENGTH MPG_CITY ENGINESIZE;
RUN;

默认阈值为0.15

结果如下：

描述性统计；

表一找了一个最能体现组间差异的变量weight写入模型，其F值最大，R²最接近1。

表二，为检验模型中变量的显著性差异，根据事先设定的显著水平（默认为0.15）。用以检查模型整体的判别能力。

第二步一开始就检验模型中已有的变量有没有冗余，能不能删除，然后再找出剩余变量中最能表现类间差异的变量加入模型中，然后检查整个模型的整体的判别能力。

重复步骤，最后：

直到不能在添加变量并且不能在删除变量为止，

最后：

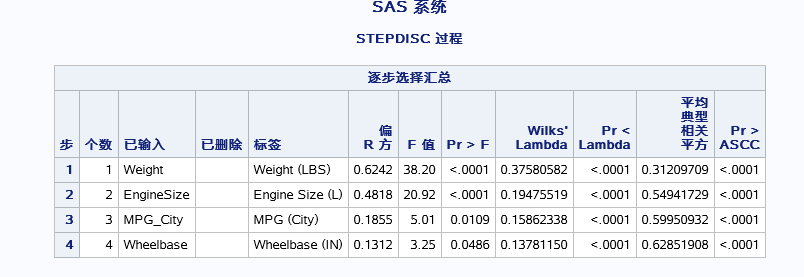
逐步分析汇总出判别最能反映出类间差异的几个分析变量。

然后在进行PROC DISCRIM过程：

PROC DISCRIM DATA=CARS_TYPES TESTDATA=CARS_TEST METHOD=NORMAL POOL=TEST
        DISTANCE LIST TESTOUT=CARS_RESULTS3;
    CLASS TYPE;
    VAR WEIGHT WHEELBASE MPG_CITY ENGINESIZE;
RUN;

结果一样。