两周前,项目里需要实现一个红心飘飘的点赞效果。抓耳挠腮了老半天,看了几篇大佬的文章,终于算是摸了个七七八八。不禁长叹一声,还是菜啊。先来看一下效果:(传送门进去点一波)

一、Bezier曲线运动轨迹
其实用大白话描述一下需求就是让一个红心图片沿着贝塞尔曲线的轨迹走,然后边走边消失。核心在于得到贝塞尔曲线上的一系列点。本文不会讲解贝塞尔曲线的原理,因为大佬们已经讲过了,而且讲的比我好。参考文章如下:
其中第二篇文章讲到了生成二阶和三阶贝塞尔曲线可以使用canvas自带的方法:quadraticCurveTo和bezierCurveTo,而高阶的则先得到曲线上一系列的点,然后顺次连接这些点来拟合高阶的贝塞尔曲线。没错,我们要的就是这一系列的点,有了这些点,就可以控制红心的轨迹了。下面是我基于作者的BezierMarker.js写的一个demo,可以直观地看出高阶贝塞尔曲线上的点:
上面100个曲线上的点坐标是由下面这段代码计算得出的:
BezierMaker.prototype.bezier = function(t) { //贝塞尔公式调用
var x = 0,
y = 0,
bezierCtrlNodesArr = this.bezierCtrlNodesArr,
n = bezierCtrlNodesArr.length - 1,
self = this
bezierCtrlNodesArr.forEach(function(item, index) {
if(!index) {
x += item.x * Math.pow(( 1 - t ), n - index) * Math.pow(t, index)
y += item.y * Math.pow(( 1 - t ), n - index) * Math.pow(t, index)
} else {
x += self.factorial(n) / self.factorial(index) / self.factorial(n - index) * item.x * Math.pow(( 1 - t ), n - index) * Math.pow(t, index)
y += self.factorial(n) / self.factorial(index) / self.factorial(n - index) * item.y * Math.pow(( 1 - t ), n - index) * Math.pow(t, index)
}
})
return {
x: x,
y: y
}
}
这个方法就是对贝塞尔公式的实现。以3阶贝塞尔公式为例(见下图),它的方程需要四个控制点(P1,P2,P3,P4)和一个t值,就能计算出曲线上的某一点的坐标。
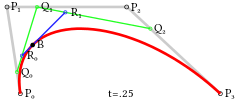
当将t由0递增到1时,就可以得到100个曲线上的点,进而拟合出相应的曲线。当我们拿到这一系列点时,其实问题已经解决了一大半了。
二、使红心飘起来
拿到拟合点数组后,绘制轨迹就是从数组中依次拿出坐标,并将红心图片绘制到相应的坐标上。并根据当前拟合点在曲线数组中的位置,改变图片的不透明度,就可以让红心飘起来了,上一部分代码,讲解见注释:
// 生成随机数
function rnd () {
let flag = Math.random() > 0.5 ? 1 : -1
return 80 * Math.random() * flag
}
class FlyHeart {
constructor (ctx, img) {
this.ctx = ctx;
this.img = heart;
// 拿到红心的运动轨迹,一系列拟合点坐标
this.bezierArr = new BezierMaker(ctx, [
{x: 187, y: 245},
{x: 170 + rnd(), y: 200},
{x: 200 + rnd() , y: 120},
{x: 140 + rnd(), y: 60}], 90).bezierArr //90表示拟合点的数量,rnd使红心的轨迹有一定的随机性
}
draw () {
// 依次取出轨迹的每个点
let position = this.bezierArr.shift();
// 清除上次画的
this.clear();
if (position) {
this.ctx.save()
// 根据当前数组长度算出透明度
this.ctx.globalAlpha = this.bezierArr.length / 30;
this.ctx.drawImage(this.img, position.x , position.y, 20, 20);
this.ctx.restore();
this.prevPosition = position;
}
}
// 清除上次画的
clear () {
if (this.prevPosition) {
this.ctx.clearRect(this.prevPosition.x, this.prevPosition.y, 20, 20);
}
}
}
接下来就是给body添加点击事件,当点击时,就新生成一个红心:
document.body.addEventListener('click', function() {
heartArr.push(new FlyHeart(ctx, heart));
})
let heartArr = []
const cvs = document.getElementById('cvs')
const ctx = cvs.getContext('2d')
const heart = document.getElementById('heart') //图片
function draw () {
if(heartArr.length) {
for(let heart of heartArr) {
heart.draw();
if(heart.bezierArr.length === 0) {
heart.clear();
let index = heartArr.indexOf(heart)
heartArr.splice(index, 1)
}
}
}
requestAnimationFrame(draw)
}
draw()
三、后记
当时看到这个需求的时候,真的是一筹莫展,看到n阶贝塞尔曲线时更是一头雾水,但是看不懂也要看,然后看着看着,看多了也就慢慢明白了。希望没浪费大家的时间,各位看官看完后有所收获(完)