【manacher】HDU3068-最长回文

【题目大意】

给出一个只由小写英文字符a,b,c...y,z组成的字符串S,求S中最长回文串的长度。

【manacher知识点】

①mx - i > P[j] 的时候，以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于 i 和 j 对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以必有 P[i] = P[j]。

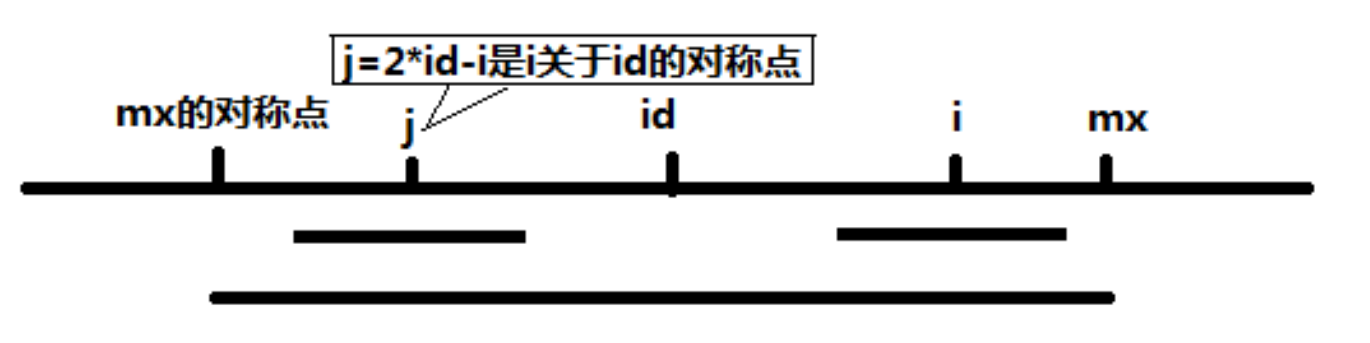
②当 P[j] > mx - i 的时候，以S[j]为中心的回文子串不完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，下图中两个绿框所包围的部分是相同的，也就是说以 S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 P[i] >= mx - i。至于mx之后的部分是否对称，就只能一个一个匹配了。

 

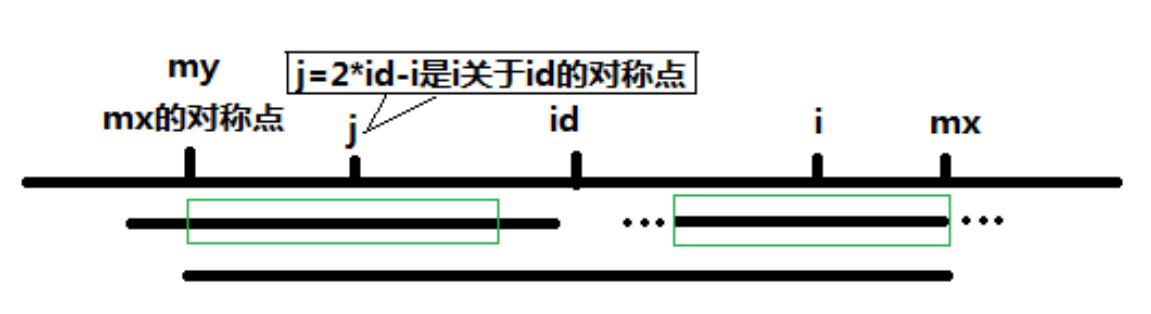
③对于 mx <= i 的情况，无法对 P[i]做更多的假设，只能P[i] = 1，然后再去匹配了

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
const int MAXN=110000+50;
char str[MAXN],s[MAXN*2];
int p[MAXN*2]; 

void init()
{
    s[0]='$';s[1]='#';
    int j=1;
    for (int i=0;str[i];i++)
    {
        s[++j]=str[i];
        s[++j]='#';
    }
    //cout<<s<<endl;
}

void solve()
{
    int mx=0,mxid=0;
    memset(p,0,sizeof(p));
    for (int i=1;s[i];i++)
    {
        if (mx>i) p[i]=(p[2*mxid-i]<(mx-i)?p[2*mxid-i]:(mx-i));
            else p[i]=1;
        while(s[i-p[i]]==s[i+p[i]]) p[i]++;
        if (i+p[i]>mx)
        {
            mx=i+p[i];
            mxid=i;
        }
    }
}

int getans()
{
    int len=strlen(str)*2+2;
    int ans=-1;
    for (int i=1;i<len;i++) ans=max(ans,p[i]);
    ans--;
    return ans;
}

int main()
{
    while (scanf("%s",str)!=EOF)
    {
        init();
        solve();
        cout<<getans()<<endl;
    }
    return 0;
}