归并排序(Merge Sort)是一种典型的基于"divide and conquer"策略的排序算法。 "divide and conquer"(分而治之,简称"分治")作为一个军事术语, 应用到归并排序中,其实包含三个步骤:分(divide), 治(conquer)和合(combine)。形象一点儿说就是,先分割包围(divide),再各个击破(conquer),最后合并战果(combine)。 归并(merge)一词可以理解为"将各个击破(conquer)与合并战果(combine)这两步糅合在一起",所谓归并,也就是将两个或两个以上的有序表合并成一个新的有序表。
在正式介绍归并排序的实现之前,先花点时间熟悉一下"divide and conquer"(分治)策略。 这里源引文章Divide-and-conquer并做中英文对照翻译。
Both merge sort and quicksort employ a common algorithmic paradigm based on recursion. This paradigm, divide-and-conquer, breaks a problem into subproblems that are similar to the original problem, recursively solves the subproblems, and finally combines the solutions to the subproblems to solve the original problem. Because divide-and-conquer solves subproblems recursively, each subproblem must be smaller than the original problem, and there must be a base case for subproblems. You should think of a divide-and-conquer algorithm as having three parts: 合并排序和快速排序均为基于递归实现的典型算法。这种称之为"分治"的算法,将问题分解成与原始问题相似的子问题,递归地解决子问题,最后将解决方案合并起来从而解决原始问题。因为分治法在解决子问题的时候是采用递归的方法,那么每一个子问题必须小于原始问题,而且每一个子问题必须能够确切地被细分到可以直接解决的粒度(注:递归返回的时刻就是子问题不可再进一步切分)。一个分治的算法包含三部分:
1. Divide the problem into a number of subproblems that are smaller instances of the same problem. 将问题切分为许多子问题,这些子问题是同一问题的较小实例。
2. Conquer the subproblems by solving them recursively. If they are small enough, solve the subproblems as base cases. 通过递归求解来解决一个个子问题。如果子问题足够小,可以将它们当做最小粒度的问题予以解决掉。
3. Combine the solutions to the subproblems into the solution for the original problem. 将子问题的解决方案合并到原始问题的解决方案之中。
You can easily remember the steps of a divide-and-conquer algorithm as divide, conquer, combine. Here's how to view one step, assuming that each divide step creates two subproblems (though some divide-and-conquer algorithms create more than two): 记住分治算法的步骤很容易,那就是"分割、击破和合并"。以下给出一个图例予以说明,假设每个分割步骤创建两个子问题(尽管一些分治算法创建了两个以上的子问题):
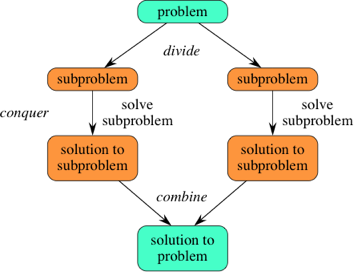
If we expand out two more recursive steps, it looks like this: 如果展开两个以上的递归步骤,看起来像这样子:

Because divide-and-conquer creates at least two subproblems, a divide-and-conquer algorithm makes multiple recursive calls. 因为分治至少创造两个子问题,所以分治算法要进行多次递归调用。
在熟悉了"divide and conquer"(分治)策略之后,我们正式切入归并排序。这里只介绍两路归并(2-way merging)。
两路归并(2-way merging)的基本思想
设两个有序表分别为A和B,其中有序表A的长度为na,有序表B的长度为nb。设表C是将有序表A和B归并后的新的有序表。变量i为表A的当前读取指针,变量j为表B的当前读取指针,变量k为表C的当前写入指针。
- 当i和j分别在表A和表B中变化时,比较A[i]和B[j]的关键字,依次把关键字小的对象写入到新表C[k]位置上去;
- 当i与j有一个已经超出了对应的表长时,将另一个表中的剩余部分照抄到新表C中去。
一旦搞清楚了两路归并的过程,实现归并排序就相当容易了。 注意:两路归并的灵魂是将两个有序表合并成一个新的有序表。两路归并的过程用C代码表示为:
1 /** 2 * Merge two sorted src list A[] and B[] to dst list C[] 3 */ 4 void merge2to1(int C[], size_t nc, int A[], size_t na, int B[], size_t nb) 5 { 6 int i = 0; /* walk list A : read */ 7 int j = 0; /* walk list B : read */ 8 int k = 0; /* walk list C : write */ 9 while (i < na && j < nb) { 10 if (A[i] < B[j]) 11 C[k++] = A[i++]; 12 else 13 C[k++] = B[j++]; 14 } 15 16 while (i < na) C[k++] = A[i++]; 17 while (j < nb) C[k++] = B[j++]; 18 }
典型的归并排序看起来是这样子滴,图片来源戳这里,

归并排序算法的分类
- 基于迭代的归并排序算法 (i.e. Bottom-up mergesort)
- 基于递归的归并排序算法 (i.e. Top-down mergesort)
基于迭代的归并排序算法(Bottom-up mergesort)
假设初始对象序列有n个对象,首先将其看做是n个长度为1的有序子序列,先做两两归并,得到(n+1)/2个长度为2的归并子序列(如果n为奇数,则最后一个有序子序列的长度为1);再做两两归并,......,如此重复,最后得到一个长度为n的有序序列。
基于递归的归并排序算法(Top-down mergesort)
与快速排序类似,归并排序也可以利用划分为子序列的方法递归实现。在递归的归并排序算法中,首先要把整个待排序序列划分为两个长度大致相等的部分,分别称之为左子表和右子表。对这些子表分别递归地进行排序,然后再把排好序的两个字表进行归并。
下面以基于递归的归并排序算法(Top-down mergesort)为例讨论归并排序的具体过程。 例如: (图片来源在这里)
1. 输入序列为 int a[] = {14,33,27,10,35,19,42,44}; 数组元素个数为8

2. 第一次分组, 8/2 = 4, {14,33,27,10} 和 {35,19,42,44}

3. 将左子表和右子表再一次分组, 4/2 = 2, { {14,33}, {27,10} } 和 { {35,19}, {42,44} }

4. 再分组, 2/2 = 1, (到这里就不能再分了), { { {14},{33} }, { {27},{10} } } 和 { { {35}, {19} }, { {42}, {44} } }

5. 分组完毕,该归并了, 第一次两两归并后,

6. 第二次两两归并后,

7. 第三次两两归并后(排序结束),

好了,现在上C代码实现。
1 /* 2 * Merge two sorted src list A[] and B[] to dst list C[] 3 */ 4 static void 5 merge2to1(int c[], size_t nc, int a[], size_t na, int b[], size_t nb) 6 { 7 if (nc < na + nb) /* error */ 8 return; 9 10 int i = 0; /* walk src list A : read */ 11 int j = 0; /* walk src list B : read */ 12 int k = 0; /* walk dst list C : write */ 13 while (i < na && j < nb) { 14 if (a[i] < b[j]) 15 c[k++] = a[i++]; 16 else 17 c[k++] = b[j++]; 18 } 19 20 while (i < na) 21 c[k++] = a[i++]; 22 23 while (j < nb) 24 c[k++] = b[j++]; 25 } 26 27 /* 28 * Merge a[l..m] and a[m+1..r] to a[l..r] 29 * l: left : 0 <= l <= n-1 30 * m: middle : 0 <= m <= n-1 31 * r: right : 0 <= r <= n-1 32 * l <= m <= r 33 */ 34 static void 35 merge(int a[], size_t n, int l, int m, int r) 36 { 37 /* 38 * NOTE: To get better performance, we can malloc aux[] 39 * out of this function, and just repeat using it 40 */ 41 int *aux = (int *)malloc(sizeof(int) * n); 42 if (aux == NULL) /* error */ 43 return; 44 45 for (int i = 0; i < n; i++) // copy a[] to aux[] 46 aux[i] = a[i]; 47 48 for (int i = l; i <= r; i++) // erase a[l..r] on purpose 49 a[i] = 0xfeedfeed; // just for better debugging 50 51 int *dc = a + l; 52 size_t ndc = n - l; 53 int *sa = aux + l; // src list a[l .. m] 54 size_t nsa = m - l + 1; // len = m - l + 1 55 int *sb = aux + m + 1; // src list b[m+1 .. r] 56 size_t nsb = r - m; // len = r - (m+1) + 1 = r - m 57 merge2to1(dc, ndc, sa, nsa, sb, nsb); 58 59 free(aux); 60 } 61 62 void 63 tdMergeSort(int a[], size_t n, int left, int right) 64 { 65 if (left >= right) 66 return; 67 68 int middle = (left + right) / 2; 69 tdMergeSort(a, n, left, middle); // make sure left is sorted 70 tdMergeSort(a, n, middle+1, right); // make sure right is sorted 71 merge(a, n, left, middle, right); // merge a[l..m] and a[m+1..r] 72 } 73 74 #define MERGESORT(a, n) tdMergeSort(a, n, 0, n-1)
完整的C代码如下:
o mergesort.c
1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <string.h> 4 5 typedef enum bool_s {false, true} bool_t; 6 7 bool_t g_isint = false; 8 9 static void show(int a[], size_t n) 10 { 11 if (g_isint) { 12 for (int i = 0; i < n; i++) 13 printf("%-2d ", a[i]); 14 } else { 15 for (int i = 0; i < n; i++) 16 printf("%-2c ", a[i]); 17 } 18 printf(" "); 19 } 20 21 /* 22 * Merge two sorted src list A[] and B[] to dst list C[] 23 */ 24 static void 25 merge2to1(int c[], size_t nc, int a[], size_t na, int b[], size_t nb) 26 { 27 if (nc < na + nb) /* error */ 28 return; 29 30 int i = 0; /* walk src list A : read */ 31 int j = 0; /* walk src list B : read */ 32 int k = 0; /* walk dst list C : write */ 33 while (i < na && j < nb) { 34 if (a[i] < b[j]) 35 c[k++] = a[i++]; 36 else 37 c[k++] = b[j++]; 38 } 39 40 while (i < na) 41 c[k++] = a[i++]; 42 43 while (j < nb) 44 c[k++] = b[j++]; 45 } 46 47 /* 48 * Merge a[l..m] and a[m+1..r] to a[l..r] 49 * l: left : 0 <= l <= n-1 50 * m: middle : 0 <= m <= n-1 51 * r: right : 0 <= r <= n-1 52 * l <= m <= r 53 */ 54 static void 55 merge(int a[], size_t n, int l, int m, int r) 56 { 57 /* 58 * NOTE: To get better performance, we can malloc aux[] 59 * out of this function, and just repeat using it 60 */ 61 int *aux = (int *)malloc(sizeof(int) * n); 62 if (aux == NULL) /* error */ 63 return; 64 65 for (int i = 0; i < n; i++) // copy a[] to aux[] 66 aux[i] = a[i]; 67 68 for (int i = l; i <= r; i++) // erase a[l..r] on purpose 69 a[i] = 0xfeedfeed; // just for better debugging 70 71 int *dc = a + l; 72 size_t ndc = n - l; 73 int *sa = aux + l; // src list a[l .. m] 74 size_t nsa = m - l + 1; // len = m - l + 1 75 int *sb = aux + m + 1; // src list b[m+1 .. r] 76 size_t nsb = r - m; // len = r - (m+1) + 1 = r - m 77 merge2to1(dc, ndc, sa, nsa, sb, nsb); 78 79 free(aux); 80 } 81 82 void 83 tdMergeSort(int a[], size_t n, int left, int right) 84 { 85 if (left >= right) { 86 printf("RETURN: %x:%x ", left, right); show(a, n); 87 88 return; 89 } 90 91 int middle = (left + right) / 2; 92 tdMergeSort(a, n, left, middle); // make sure left is sorted 93 tdMergeSort(a, n, middle+1, right); // make sure right is sorted 94 merge(a, n, left, middle, right); // merge a[l..m] and a[m+1..r] 95 96 printf(" MERGE: %x:%x:%x ", left, middle, right); show(a, n); 97 } 98 99 #define MERGESORT(a, n) tdMergeSort(a, n, 0, n-1) 100 101 int 102 main(int argc, char *argv[]) 103 { 104 if (argc < 2) { 105 fprintf(stderr, "Usage: %s <C1> [C2] ... ", argv[0]); 106 return -1; 107 } 108 109 argc--; 110 argv++; 111 112 int n = argc; 113 int *a = (int *)malloc(sizeof(int) * n); 114 #define VALIDATE(p) do { if (p == NULL) return -1; } while (0) 115 VALIDATE(a); 116 117 char *s = getenv("ISINT"); 118 if (s != NULL && strncmp(s, "true", 4) == 0) 119 g_isint = true; 120 121 if (g_isint) { 122 for (int i = 0; i < n; i++) 123 *(a+i) = atoi(argv[i]); 124 } else { 125 for (int i = 0; i < n; i++) 126 *(a+i) = argv[i][0]; 127 } 128 129 printf(" "); 130 for (int i = 0; i < n; i++) 131 printf("%-2x ", i); 132 printf(" "); 133 134 printf("Before sorting: "); show(a, n); 135 MERGESORT(a, n); 136 printf("After sorting: "); show(a, n); 137 138 #define FREE(p) do { free(p); p = NULL; } while (0) 139 FREE(a); 140 return 0; 141 }
o 编译并测试
$ gcc -g -Wall -m32 -std=c99 -o mergesort mergesort.c 4 $ ISINT=true > ./mergesort 14 33 27 10 35 19 42 44 0 1 2 3 4 5 6 7 Before sorting: 14 33 27 10 35 19 42 44 RETURN: 0:0 14 33 27 10 35 19 42 44 RETURN: 1:1 14 33 27 10 35 19 42 44 MERGE: 0:0:1 14 33 27 10 35 19 42 44 RETURN: 2:2 14 33 27 10 35 19 42 44 RETURN: 3:3 14 33 27 10 35 19 42 44 MERGE: 2:2:3 14 33 10 27 35 19 42 44 MERGE: 0:1:3 10 14 27 33 35 19 42 44 RETURN: 4:4 10 14 27 33 35 19 42 44 RETURN: 5:5 10 14 27 33 35 19 42 44 MERGE: 4:4:5 10 14 27 33 19 35 42 44 RETURN: 6:6 10 14 27 33 19 35 42 44 RETURN: 7:7 10 14 27 33 19 35 42 44 MERGE: 6:6:7 10 14 27 33 19 35 42 44 MERGE: 4:5:7 10 14 27 33 19 35 42 44 MERGE: 0:3:7 10 14 19 27 33 35 42 44 After sorting: 10 14 19 27 33 35 42 44 $ ./mergesort M E R G E S O R T E X A M P L E 0 1 2 3 4 5 6 7 8 9 a b c d e f Before sorting: M E R G E S O R T E X A M P L E RETURN: 0:0 M E R G E S O R T E X A M P L E RETURN: 1:1 M E R G E S O R T E X A M P L E MERGE: 0:0:1 E M R G E S O R T E X A M P L E RETURN: 2:2 E M R G E S O R T E X A M P L E RETURN: 3:3 E M R G E S O R T E X A M P L E MERGE: 2:2:3 E M G R E S O R T E X A M P L E MERGE: 0:1:3 E G M R E S O R T E X A M P L E RETURN: 4:4 E G M R E S O R T E X A M P L E RETURN: 5:5 E G M R E S O R T E X A M P L E MERGE: 4:4:5 E G M R E S O R T E X A M P L E RETURN: 6:6 E G M R E S O R T E X A M P L E RETURN: 7:7 E G M R E S O R T E X A M P L E MERGE: 6:6:7 E G M R E S O R T E X A M P L E MERGE: 4:5:7 E G M R E O R S T E X A M P L E MERGE: 0:3:7 E E G M O R R S T E X A M P L E RETURN: 8:8 E E G M O R R S T E X A M P L E RETURN: 9:9 E E G M O R R S T E X A M P L E MERGE: 8:8:9 E E G M O R R S E T X A M P L E RETURN: a:a E E G M O R R S E T X A M P L E RETURN: b:b E E G M O R R S E T X A M P L E MERGE: a:a:b E E G M O R R S E T A X M P L E MERGE: 8:9:b E E G M O R R S A E T X M P L E RETURN: c:c E E G M O R R S A E T X M P L E RETURN: d:d E E G M O R R S A E T X M P L E MERGE: c:c:d E E G M O R R S A E T X M P L E RETURN: e:e E E G M O R R S A E T X M P L E RETURN: f:f E E G M O R R S A E T X M P L E MERGE: e:e:f E E G M O R R S A E T X M P E L MERGE: c:d:f E E G M O R R S A E T X E L M P MERGE: 8:b:f E E G M O R R S A E E L M P T X MERGE: 0:7:f A E E E E G L M M O P R R S T X After sorting: A E E E E G L M M O P R R S T X
上面倒数第一个归并排序过程用图表示如下(截图来自《算法》第4版)

最后,有必要提一下归并排序的时间复杂度和空间复杂度。 注意: 归并排序是一种稳定的排序算法。
Worst-case performance O(N * logN)
Best-case performance O(N * logN) typical, O(N) natural variant
Average performance O(N * logN)
Worst-case space complexity О(N) total, O(N) auxiliary
参考资料:
- Data Structures - Merge Sort Algorithm
- Computer Algorithms: Merge Sort
- Overview of merge sort
- Merge Sort using Java with program code
- The Merge Sort
- Merge sort from Wikipedia
小结:
归并排序(Merge Sort)分为两种,一种是基于迭代的归并排序算法,也就是自底向上的归并排序(Bottom-up mergesort); 另一种就是基于递归的归并排序算法,也就是自顶向下的归并排序算法(Top-down mergesort)。 本文讨论的是后一种算法并给出了相应的C代码实现,因为递归实现的归并排序是算法设计中分治思想的典型应用(来自算法一书的原文: The recursive implementation of mergesort is prototypical of the divide-and-conquer algorithm design paradigm, where we solve a large problem by dividing it into pieces, solving the subproblems, then using the solutions for the pieces to solve the whole problem.)。无论是Bootom-up还是Top-down的算法,牢记两路归并的灵魂是将两个有序表合并成一个新的有序表,也就掌握了这一算法的根本。 下一节将介绍基数排序(Radix Sort)。