本文作者:i春秋作家——jishuzhain
一些反反编译技术的简单例子
在以前的时代,对软件来进行下(汇编级)逆向工程确实是一个很繁琐的过程,但是如今现代反编译器的发展已经把这个过程变得容易了。只需要在编译过后的机器代码中使用反编译器的功能就可以把机器代码尝试恢复到近似于软件以前的源代码级别。
不可否认的是,支持反汇编功能的反编译器的这种技术它背后的科学和便利性是很值得赞赏的。就像这样,在点击功能选项时,一个完完全全的新手可以将难懂的“机器代码”转换成人类可读的代码,然后就能上手逆向工程了,你说,惊不惊讶?
然而现实情况是,安全研究人员也越来越依赖于这些技术,虽然工欲善其事必先利其器这句话没错,但是越依赖工具,这将使我们更加地暴露在这些工具的不完善之处。在这篇文章中,我将探讨一些和反编译器相关的破坏或有目的性地会误导逆向工程师的反反编译技术,敬请期待。
Positive SP Value
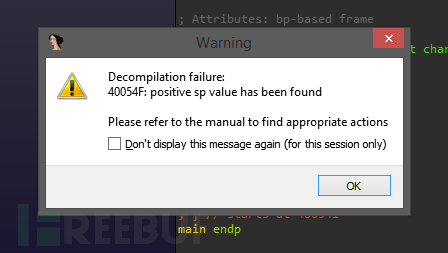
第一种技术是能破坏Hex-Rays反编译器的经典方法,在IDA Pro中,如果在返回之前没有清理堆栈分配(平衡堆栈指针),则反编译器将拒绝反编译该函数。
比如 无法F5时的解决
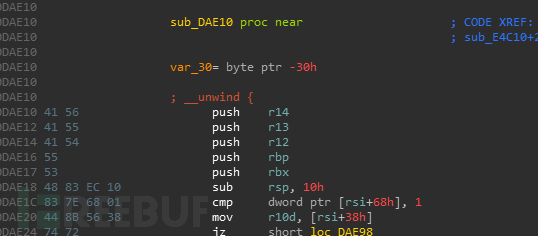
这样的情况一般是程序代码有一些干扰代码,让IDA的反汇编分析出现错误。比如用push + n条指令 + retn来实际跳转,而IDA会以为retn是函数要结束,结果它分析后发现调用栈不平衡,因此就提示sp analysis failed。
例如当IDA无法合理地构造出某些函数调用时的定义类型时偶尔也会发生这种情况,作为反反编译技术,开发人员可以通过使用一些特殊的手法来破坏堆栈指针的平衡,以此诱导逆向者来出现这些效果。
//
// compiled on Ubuntu 16.04 with:
// gcc -o predicate predicate.c -masm=intel
//
#include <stdio.h>
#define positive_sp_predicate
__asm__ (" push rax "
" xor eax, eax "
" jz opaque "
" add rsp, 4 "
"opaque: "
" pop rax ");
void protected()
{
positive_sp_predicate;
puts("Can't decompile this function");
}
void main()
{
protected();
}
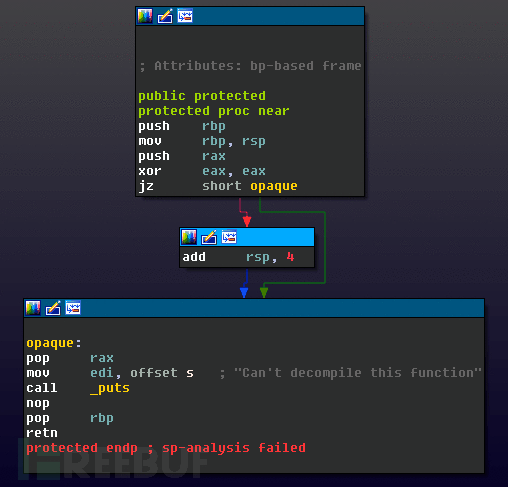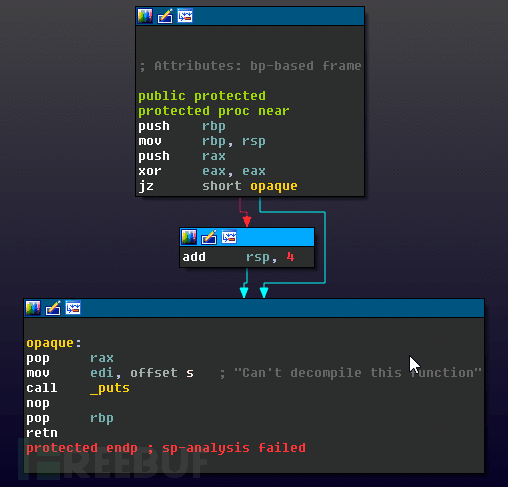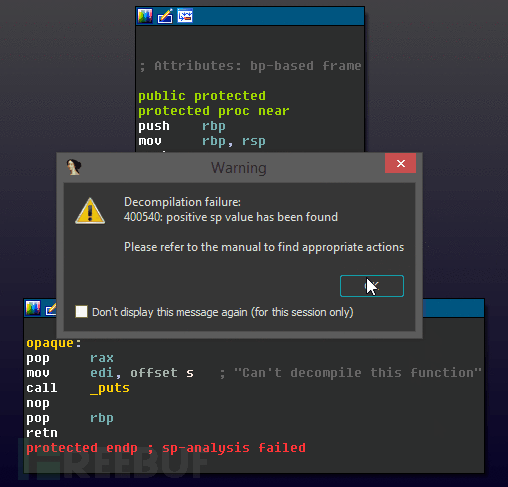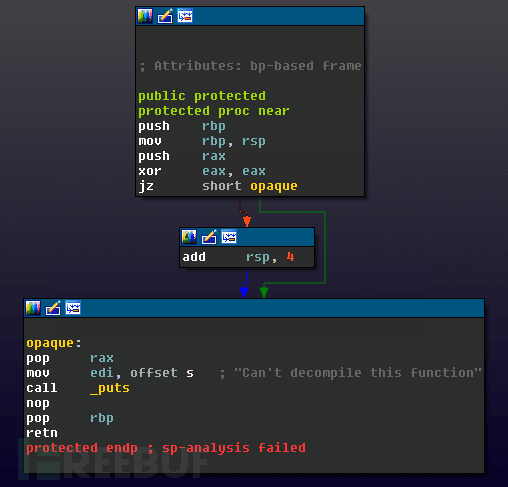
上面定义add rsp, 4的positive_sp_predicate宏中的指令永远不会在运行时被执行,但是它会使IDA进行反编译时的静态分析失败。当试图反编译protected()提供的生成函数会产生以下结果:
这种技术是比较有名的,可以通过修补缺陷来修复,也可以通过手动修正堆栈偏移值来修复。
在MBE中,有使用这种技术作为一个简单的技巧来阻止新手逆向工程师(例如学生)来进行反汇编并能直接让反编译器输出软件的源代码来。
返回型劫持
现代反编译器希望的是能准确地识别和抽象出编译器生成的低级的能记录的逻辑信息,例如功能的开头/结尾或能控制的流(元)数据部分。
反编译器力图从输出中来省略这些信息,因为保存这些寄存器或管理堆栈帧分配的任务并不会在反编译器输出软件源代码时得到执行。
这些遗漏(或者是Hex-Rays反编译器启发式方法中的一个缺陷)的一个有趣的地方是我们可以在函数返回之前来“移动”栈,使得反编译器不发出警告或者也不显示任何带有恶意的指示。
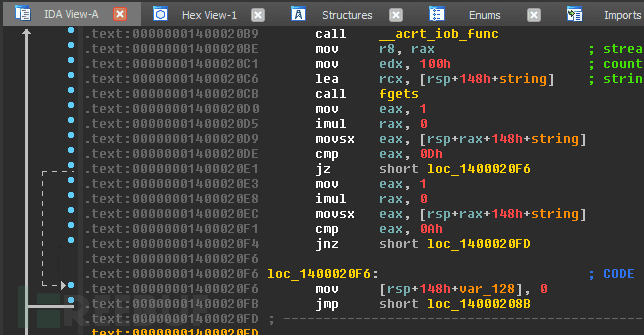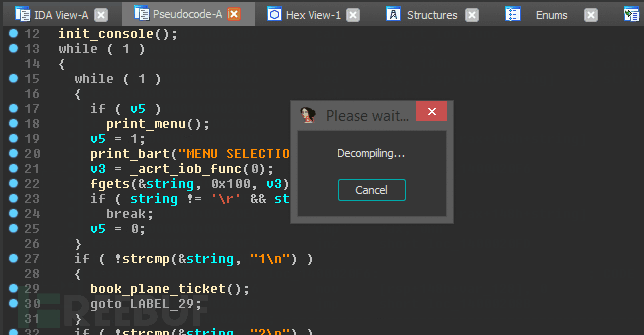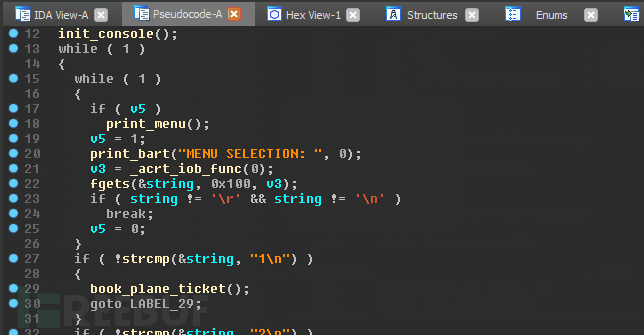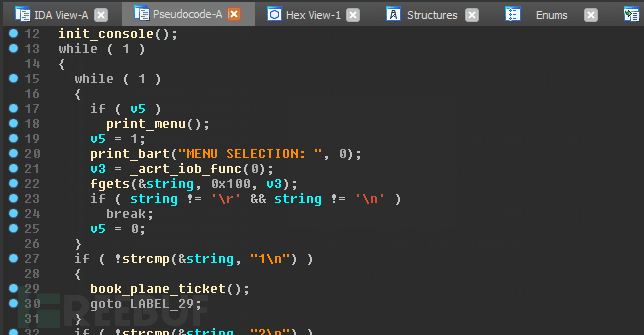
Stack pivot 是二进制开发中常用的技术,可以实现任意的ROP。在这种情况下,我们(作为开发人员)使用它作为一种手段,来从不知情的逆向工程师手中劫持到执行权。可以说,那些专注于反编译器输出结果的人肯定不会注意到它,哈哈。
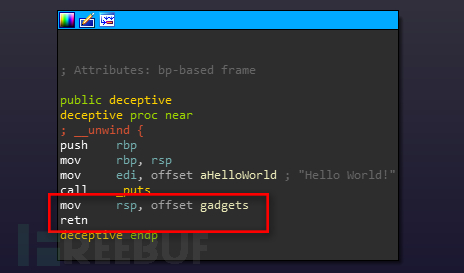
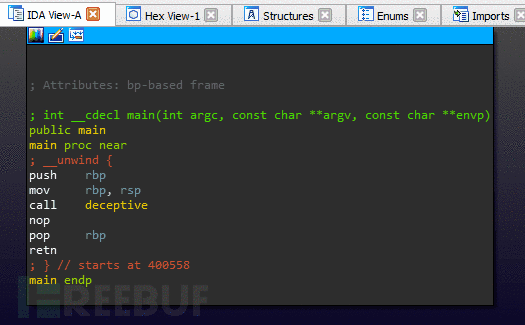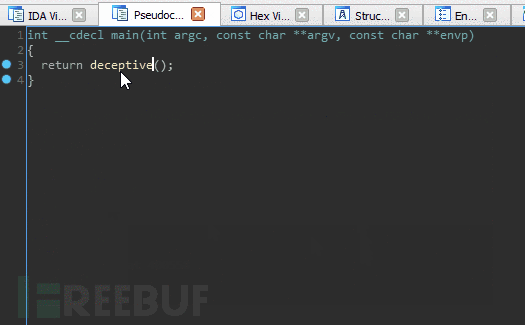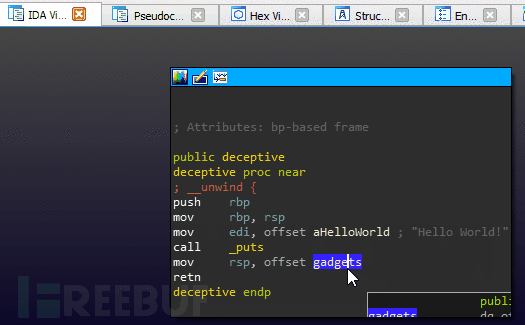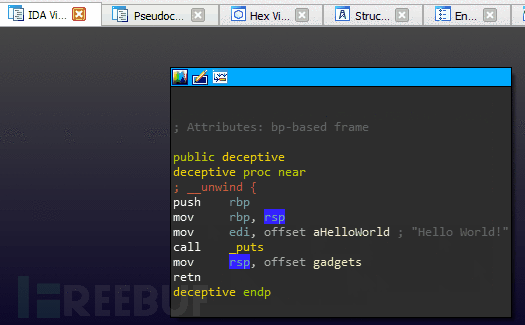
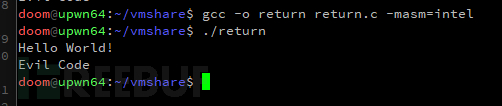
我们把这个堆栈转换成一个很小的ROP链,这个链已经被编译成二进制文件来执行这个错误操作了。最终结果是一个对反编译器“不可见”的函数调用。图中我们调用函数的目的只是打印出“恶意代码”来证明它已经被执行。
图: 利用返回劫持反编译技术执行编译后的二进制文件
@[用于演示这种从反编译器中隐藏代码的技术的代码可以在下面找到]
//
// compiled on Ubuntu 16.04 with:
// gcc -o return return.c -masm=intel
//
#include <stdio.h>
void evil() {
puts("Evil Code");
}
extern void gadget();
__asm__ (".global gadget "
"gadget: "
" pop rax "
" mov rsp, rbp "
" call rax "
" pop rbp "
" ret ");
void * gadgets[] = {gadget, evil};
void deceptive() {
puts("Hello World!");
__asm__("mov rsp, %0; "
"ret"
:
:"i" (gadgets));
}
void main() {
deceptive();
}
滥用 ‘noreturn’ 函数
我们将介绍的最后一个技巧是利用IDA的自动感知功能将函数标记为noreturn,因为每一个的noreturn函数将会表示为从标准库来的exit()或者abort()这些函数。
在生成给定函数的伪代码时,反编译器会在调用noreturn函数后丢弃任何代码。能预计到的是即使使用的是exit()函数,对于其他任何一个函数它都不会返回并继续执行代码。
**图:**直接在调用noreturn函数之后的代码对于反编译器是不可见的
如果恶意攻击者可以欺骗IDA让它相信一个函数是noreturn,但实际上这个函数它并不是noreturn的时候,那么这个恶意行为者可以悄悄地将恶意代码隐藏起来。
下面的例子演示了我们可以通过多种方法实现这个效果。
//
// compiled on Ubuntu 16.04 with:
// gcc -o noreturn noreturn.c
//
#include <stdio.h>
#include <stdlib.h>
void ignore() {
exit(0); // force a PLT/GOT entry for exit()
}
void deceptive() {
puts("Hello World!");
srand(0); // post-processing will swap srand() <--> exit()
puts("Evil Code");
}
void main() {
deceptive(); }
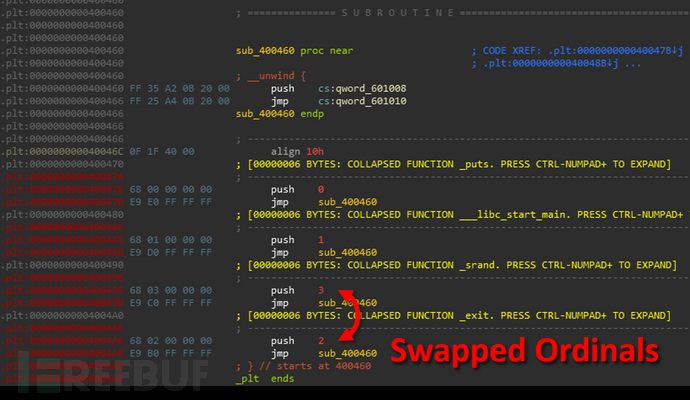
通过编译上面的代码,并根据生成的二进制文件运行一个简短的基于二进制的后期处理脚本,我们可以在过程连接表中交换推送的序号。这些索引用于软件在运行时解析库的导入。
在这个例子中,我们交换了srand()与exit()的序号。因此,IDA认为deceptive()修改后的二进制文件中的exit()的noreturn函数才是调用函数,而srand()不是调用函数。
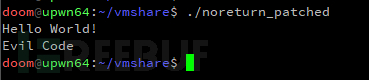
我们在IDA中看到exit()被调用,而srand()在运行,事实上srand()是不可控的。对反编译器的影响程度几乎与上一节所描述的返回劫持技术相同。运行的二进制文件表明我们的“恶意代码”也正在执行,而反编译器对此却并不知情。
虽然在这些例子中存在恶意代码,但将这些技术使用在具有更大的功能和复杂的条件下时,将使得它们非常容易上手,并造成更大危害。
结论
反编译器是一个令人印象很深刻但却又不完善的技术。它在不完整的信息上来进行一些操作,尽其所能地来输出接近于我们认知的软件源代码。恶意行为者同时可以(也将会)利用这些不对称的技术手段来作为欺骗手法去对用户进行一些恶意攻击(行为)。
随着行业越来越依赖于反编译器(工具),反反编译技术的采用将会与反调试一样地快速增加和发展起来,谢谢阅读。欢迎与我交流~
转自:https://blog.ret2.io/2017/11/16/dangers-of-the-decompiler