将内层位移换算到外层
在3维场景功能实现中,需要制作有类似于UG中使用坐标系来转动和平移节点的功能,在实现过程发现:
如果将平移层置于旋转功能层内,则:旋转时,如果事先经过了平移操作,将导致节点在场景中甩动,而不在移动中心转动;
如果将平移动层置于旋转功能层外,则:平移时,如果事先经过了旋转,将导致节点在场景中非坐标轴方向平移,而不是按原传感器方向平移。
另外,若使用分层的方式实现绕轴旋转,则在内层坐标旋转之后,外层旋转时将不在坐标轴上,而是空间的任意轴。(这一条是在实现时才发现的,空间意识还是不够强!-_-“)
思考之后,方案如下:
由于同一层次的“旋转”在“位移”之前计算,我们由外到内布置三层原始数据的坐标层,依次为:真实旋转、平衡层;临时旋转层;临时平移层。
在每次内层平移(保证按坐标轴平移)完成之后,将内层的平移数据,换算到外层,再将内层数据和传感器状态复位到平移开始时的状态,以保证内层节点位置相对世界坐标系不变,且不影响旋转(不至产生甩动现象)和下次平移。
在每次中间层完成旋转之后,将中间层旋转数据换算到外层,再将中间层数据和传感器状态复位到旋转开始时的状态,以保证中间层旋转角相对世界坐标系不变,且不影响平移和旋转。
具体做法分两种:
其一,在场景内部以脚本方式转换,不需要组件参与;
其二,在场景中将传感器取得的值路由给组件,然后利用引擎内置算法处理,再将值设置到场景中,涉及到较多交互。
若采用做法一,则可以使用引擎接口计算矩阵,免去不少繁锁的算法;若采用方法二,则需要在脚本中完成旋转矩阵中的相关算法,经过偿试,在矩阵换算之后,再将矩阵换算回四元数(即空间任意轴的旋转)过于繁杂,最终选择做法一。以下是做法一探索时,用到过的大部分算法,矩阵换算回四元数的算法未记录。
一、旋转算法
问题一:XYZ空间内某点绕X、Y、Z轴旋转一次
这个问题比较简单,网上已经有较多总结:
设旋转前坐标为 ,旋转后坐标为
,旋转后坐标为 。
。
1.绕Z轴旋转γ角
公式表示:
x′=cosγ⋅x−sinγ⋅y
y′=sinγ⋅x+coγ⋅y
z′=z
最后是代码表示
|
//将空间点绕Z轴旋转
//输入参数 x y为空间点原始x y坐标
//thetaz为空间点绕Z轴旋转多少度,角度制范围在-180到180
//outx outy为旋转后的结果坐标
void codeRotateByZ(double x, double y, double thetaz, double& outx, double& outy)
{
double x1 = x;//将变量拷贝一次,保证&x == &outx这种情况下也能计算正确
double y1 = y;
double rz = thetaz * CV_PI / 180;
outx = cos(rz) * x1 - sin(rz) * y1;
outy = sin(rz) * x1 + cos(rz) * y1;
}
|
2.绕Y轴旋转β角
公式表示:
x′=cosβ⋅x+sinβ⋅z
y′=y
z′=−sinβ⋅x+cosβ⋅z
最后是代码表示
|
//将空间点绕Y轴旋转
//输入参数 x z为空间点原始x z坐标
//thetay为空间点绕Y轴旋转多少度,角度制范围在-180到180
//outx outz为旋转后的结果坐标
void codeRotateByY(double x, double z, double thetay, double& outx, double& outz)
{
double x1 = x;
double z1 = z;
double ry = thetay * CV_PI / 180;
outx = cos(ry) * x1 + sin(ry) * z1;
outz = cos(ry) * z1 - sin(ry) * x1;
}
|
3.绕X轴旋转α角
公式表示:
x′=x
y′=cosα⋅y−sinα⋅z
z′=sinα⋅y+cosα⋅z
最后是代码表示
|
//将空间点绕X轴旋转
//输入参数 y z为空间点原始y z坐标
//thetax为空间点绕X轴旋转多少度,角度制范围在-180到180
//outy outz为旋转后的结果坐标
void codeRotateByX(double y, double z, double thetax, double& outy, double& outz)
{
double y1 = y;//将变量拷贝一次,保证&y == &y这种情况下也能计算正确
double z1 = z;
double rx = thetax * CV_PI / 180;
outy = cos(rx) * y1 - sin(rx) * z1;
outz = cos(rx) * z1 + sin(rx) * y1;
}
|
问题二:空间点绕任意轴旋转
对于这三个特殊的旋转轴我们已经有了解决方案了,现在对于任意的轴 要怎么办呢?我们可以将这个旋转分解:
-
- 将整个坐标轴旋转,使得旋转轴 和 轴重合
- 再将点 绕 轴旋转 角
- 再将整个坐标轴旋转回原位
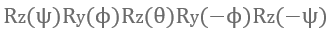
易得旋转矩阵
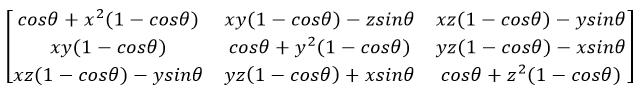
首先,需要定义"任意轴"的单位向量,例如X轴可以用向量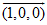 来表示。
来表示。
那么假设旋转轴的单位向量为 ,旋转前坐标为
,旋转前坐标为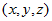 ,旋转后坐标为
,旋转后坐标为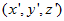 ,旋转角为
,旋转角为 ,于是有:
,于是有:
x′=(vx⋅vx⋅(1−cosθ)+cosθ)⋅x+(vx⋅vy⋅(1−cosθ)−vz⋅sinθ)⋅y+(vx⋅vz⋅(1−cosθ)+vy⋅sinθ)⋅z
y′=(vx⋅vy⋅(1−cosθ)+vz⋅sinθ)⋅x+(vy⋅vy⋅(1−cosθ)+cosθ)⋅y+(vy⋅vz⋅(1−cosθ)−vx⋅sinθ)⋅z
z′=(vx⋅vz⋅(1−cosθ)−vy⋅sinθ)⋅x+(vy⋅vz⋅(1−cosθ)+vx⋅sinθ)⋅y+(vz⋅vz⋅(1−cosθ)+cosθ)⋅z
计算时照着公式代入即可。
最后给出代码实现:
|
//定义返回结构体
struct Point3f
{
Point3f(double _x, double _y, double _z)
{
x = _x;
y = _y;
z = _z;
}
double x;
double y;
double z;
};
//点绕任意向量旋转,右手系
//输入参数old_x,old_y,old_z为旋转前空间点的坐标
//vx,vy,vz为旋转轴向量
//theta为旋转角度角度制,范围在-180到180
//返回值为旋转后坐标点
Point3f RotateByVector(double old_x, double old_y, double old_z, double vx, double vy, double vz, double theta)
{
double r = theta * CV_PI / 180;
double c = cos(r);
double s = sin(r);
double new_x = (vx*vx*(1 - c) + c) * old_x + (vx*vy*(1 - c) - vz*s) * old_y + (vx*vz*(1 - c) + vy*s) * old_z;
double new_y = (vy*vx*(1 - c) + vz*s) * old_x + (vy*vy*(1 - c) + c) * old_y + (vy*vz*(1 - c) - vx*s) * old_z;
double new_z = (vx*vz*(1 - c) - vy*s) * old_x + (vy*vz*(1 - c) + vx*s) * old_y + (vz*vz*(1 - c) + c) * old_z;
return Point3f(new_x, new_y, new_z);
}
|
二、欧拉角
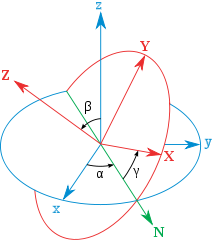
欧拉角:即以下三角的合集,用于确定的描述定点转动。
贝塔:章动角;
阿尔法:进动角;
伽马:自转角。
三、矩阵乘法
略
![]()
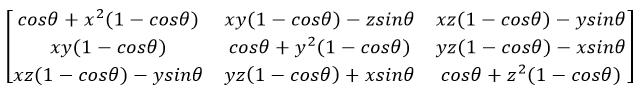
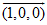 来表示。
来表示。 ,旋转前坐标为
,旋转前坐标为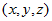 ,旋转后坐标为
,旋转后坐标为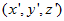 ,旋转角为
,旋转角为 ,于是有:
,于是有:

