运筹学那些事，专科学生学习运筹学之图论方法，No.7

文章目录

• 图的基本概念
• 树和树的逐步生成法
• 最小枝杈树问题
• 最短路线问题
• 最大流量问题
• 自考说明

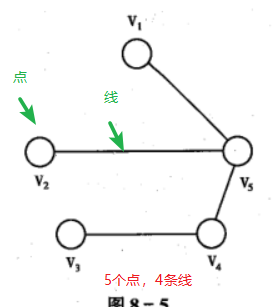
图的基本概念

图的最基本要素是：

1. 点以及点之间的一些连线（简称线或者边）
2. 带箭头的线（有向线）
3. 在图的点旁或边旁标上数（有时称之为杈）

树和树的逐步生成法

树需要满足2个基本条件

1. 连通的
2. 不含圈

一个性质：任何一个树中的线数必定是它的点数减1

最小枝杈树问题

概念

最小枝杈树问题是关于在一个网络中，从一个起点出发到所有点，找出一条或几条路线，以使在这样一些路线中所采用的全部支线的总长度是最小的，或敷设费用最少

该处提到了两种方法，普赖姆法 和 克鲁斯喀尔法 。 自考的重点是 普赖姆法

下面是一个在住宅区安装供水管的案例

最小枝杈树算法是按把最近的未接点来接到那些已接点上去的方法来进行的。连接方法如下

1. 从始点出发，找到和1最近的节点，将1 - 3 连接好
   
2. 从已接节点1、3出发，找到和1、3最近的节点，发现4与1距离最近，连接1 - 4
   
3. 从已接点1、3、4出发，找到与1、3、4最近的，发现7与1距离最近，将7与1连接
   
4. 从已接点1、3、4、7出发，找到节点最近的节点，发现5与3距离最近，连接
   
5. 相同的方法，找到5、6之间的距离最短
   
   最终得到如下图示
   

最短路线问题

当通过网络的各边所需的时间、距离或费用为已知时，找到从入口(s)到出口(t)所需的最少时间，最短距离或最少费用的路径问题，这些问题称作网络的路线问题。

最短路线问题计算方法
从终点开始逐步逆向推算

从终点开始推算之后，得到最小的里程是650，这个就是最短路线

最大流量问题

当以物体、能量或信息等作为流量流过网络时，怎样使流过网络的流量最大，或者使流过网络的流量的费用或时间最小。通常把设计这样的流量模型问题，叫做网络的流量问题。

自考对于本节，目前还未涉及 最大流量问题相关计算题，可以选看

自考说明

本节在自考部分，主要涉及的题目是最小枝杈树与最短距离，两个重点，在本套课程结束之后，有专门针对于这部分的复习内容。

更多内容，欢迎关注 https://dwz.cn/r4lCXEuL