2018-07-08 13:24:31
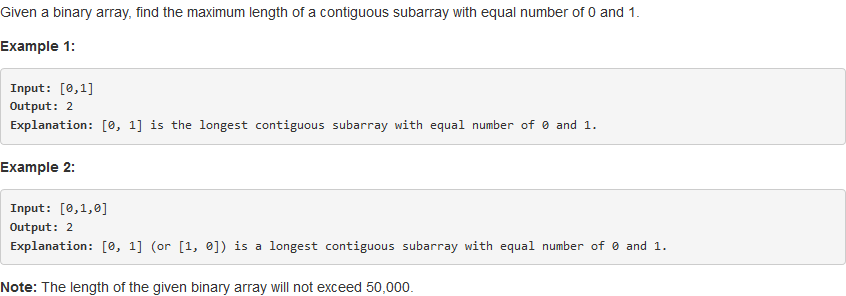
一、525. Contiguous Array
问题描述:
问题求解:
我们都知道对于subarray的问题,暴力求解的时间复杂度为O(n ^ 2),问题规模已经给出是50000量级,显然只能是O(n),至多O(nlogn)的复杂度。
本题使用DP和滑动数组都比较棘手,这才是最麻烦的地方,我们知道一般来说对于subarray的问题,dp和滑动数组是两大利器,但是本题这两个最实用的解法都不再适用,那么该如何解决呢?
其实想通了就是一个很简单的问题,本题是longest target sum subarray的变种题,核心的思路就是进行一步转化,如果把0变成-1,那么原题就变成了求target sum == 0的最长子数组。
这里给出的方案是preSum + HashMap的策略来进行解决,可以说方法是比较巧妙的。
public int findMaxLength(int[] nums) {
int res = 0;
HashMap<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) if (nums[i] == 0) nums[i] = -1;
int sum = 0;
map.put(0, -1);
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
if (map.containsKey(sum)) res = Math.max(res, i - map.get(sum));
else map.put(sum, i);
}
return res;
}
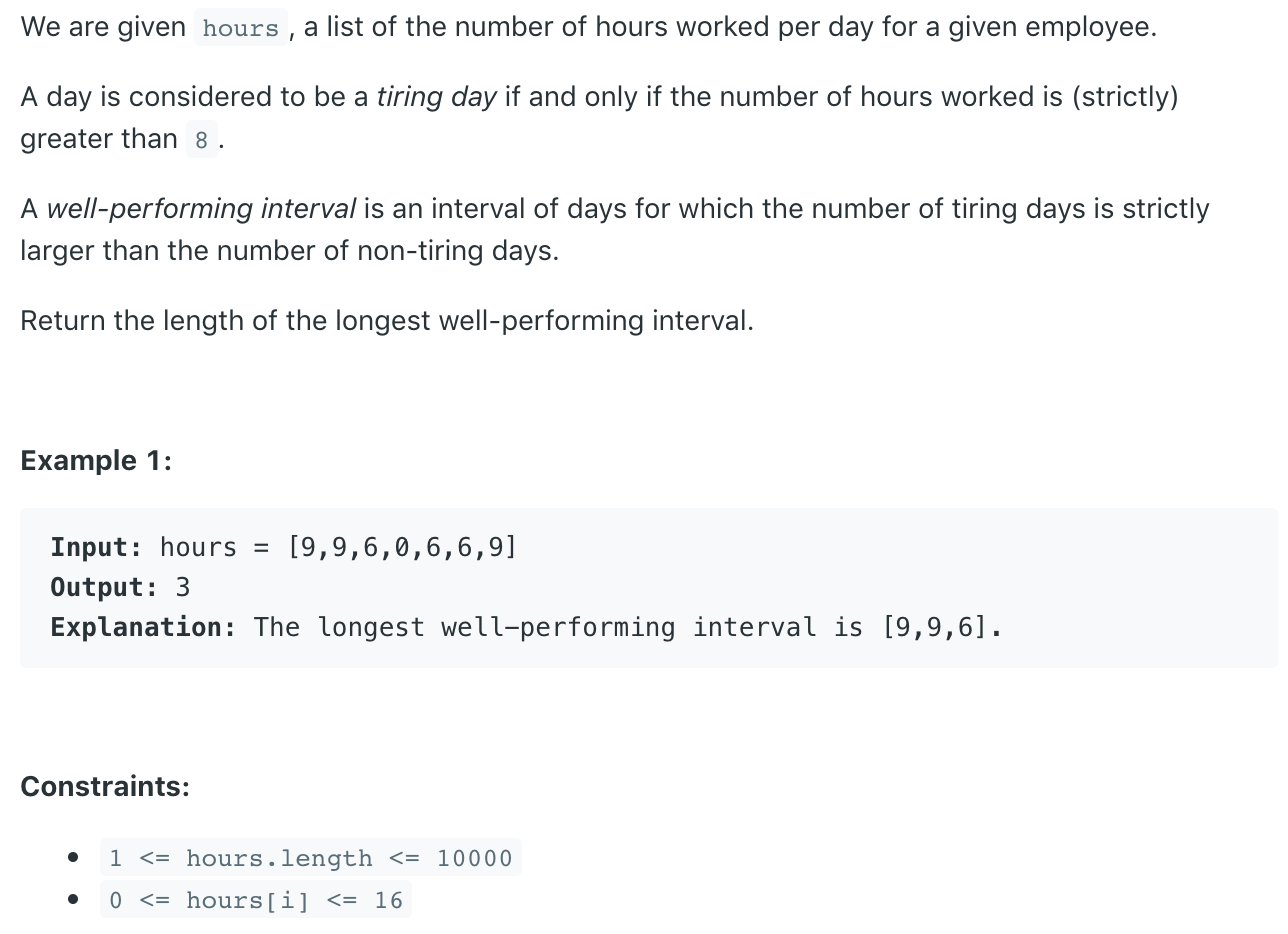
二、1124. Longest Well-Performing Interval
问题求解:
问题求解:
无独有偶,leetcode最近的contest中出了一题非常类似的问题,本质上依然是最长target sum的子数组,当时的想法也是陷入了范式中,错误的认为子数组的问题都可以使用dp或者滑动数组进行求解,导致走入了死胡同。
本题也是一条变种题,可见如何直接出subarray of target sum 是没有多大的价值的,这个题目直接问的话,就非常简单直白,很容易就会想到使用hashmap去求解,但是如果进行一下包装,就未必能想到了。
总之,碰到subarray的问题,不仅要能联想到dp/sliding window,还要有意识去想想其他的解法。
public int longestWPI(int[] hours) {
if (hours.length == 0) return 0;
int n = hours.length;
int res = 0;
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < n; i++) {
if (hours[i] > 8) hours[i] = 1;
else hours[i] = -1;
}
int curSum = 0;
for (int i = 0; i < n; i++) {
curSum += hours[i];
if (curSum >= 1) res = Math.max(res, i + 1);
if (map.containsKey(curSum - 1)) res = Math.max(res, i - map.get(curSum - 1));
map.put(curSum, map.getOrDefault(curSum, i));
}
return res;
}