二分法的时间复杂度是O(logn),所以在算法中,比O(n)更优的时间复杂度几乎只能是O(logn)的二分法。
根据时间复杂渡来倒推算法也是面试中的常用策略:题目中若要求算法的时间复杂度是O(logn),那么这个算法基本上就是二分法。
在这里,我们不做二分法的基本概念介绍,直接给出实现二分最基本的代码。具体理由看注释。
在这里特别说明:
在二分法中的while循环只是用于缩小查找范围,直至缩小到我们能够直接可辩别的范围内。而最后结果的return是依靠最后的if语句来比较并实现的。
1 class solution{ 2 3 public: 4 int binarySearch(int nums[], int target) 5 { 6 //判断传入的数组不为空 7 if(nums == NULL || sizeof(nums) / sizeof(int) == 0) 8 { 9 return -1; 10 } 11 12 int len = sizeof(nums) / sizeof(int); 13 int start = 0; 14 int end = len - 1; 15 16 17 //这里判断条件是start + 1< end 18 //终止时是start + 1 = end; 19 //这样终止时是start和end是相邻的两个下标。 20 21 //注意:我们并没有在while语句里面直接得到并return 22 //while只是缩小了区间范围 23 //而是把范围缩小到了我们易于操作的两个索引的范围内, 24 //并且通过后面的if语句来判断并return 25 while(start + 1 < end) 26 { 27 //这里没有采用middli = (start + end) / 2; 28 //原因是避免当start和end很大的时候形成溢出 29 int middle = start + (start - end) / 2; 30 31 if(nums[midddle] == target) 32 { 33 middle = end; 34 } 35 else if(nums[middle] < target) 36 { 37 start = middle + 1; 38 } 39 40 else 41 { 42 end = middle - 1; 43 } 44 45 } 46 47 if(nums[start] == target) 48 { 49 return start; 50 } 51 if(nums[end] == target) 52 { 53 return end; 54 } 55 else 56 { 57 return -1; 58 } 59 60 61 } 62 63 int binarySearch_v2(int nums[], int target) 64 { 65 if(nums == NULL || sizeof(nums) / sizeof(int) == 0) 66 { 67 return -1; 68 } 69 70 int len = sizeof(nums) / sizeof(int); 71 int start = 0; 72 int end = len - 1; 73 74 //这里判断语句是start < end; 75 //跳出循环时start = end 76 //所以在后面的if语句判断中只有nums[start] == target 77 78 //因为int middle = start + (start - end) / 2具有向左靠拢的性质 79 //所以这里的更新条件为start = middle + 1, end = middle - 1 80 while(start < end) 81 { 82 int middle = start + (start - end) / 2; 83 84 if(nums[middle] == target) 85 { 86 start = middle; 87 } 88 else if(nums[middle] < target) 89 { 90 start = middle + 1; 91 } 92 else: 93 { 94 end = middle - 1; 95 } 96 } 97 98 if(nums[start] = target) 99 { 100 return start; 101 } 102 else: 103 { 104 return -1; 105 } 106 107 108 } 109 }
二,二分位置之OOXX
在这种题目中,可以将OO视为不满足某个条件,而将XX视为满足某个条件,这样就可以把一个数组或者序列分为OO....OOXX....XX类型。而这样的题目往往是给出一个数组,要求找出数组中第一个/最后一个满足条件的位置。
OOOOO....OOOXXX...XXXXX
对于这样的题目可以采用二分法进行。

三:在一个经过排序的数组元素超级多的数组中找出目标元素。
解决这样的问题,方式一:暴力求解,直接按顺序去除数组中元素与目标值target进行比较,这样的算法的时间复杂度是O(n),当然,在生活中也是不愿意看到的。方式二:二分法求解。
我们先来说明c++中vector的实现原理,然后将这样的原理移植到我们的二分算法中。

三:找出经过旋转后的排序数组中的最小值
例题:假设一个排好序的数组在其某一未知点发生了旋转(比如0 1 2 4 5 6 7 可能变成4 5 6 7 0 1 2)。你需要找到其中最小的元素。
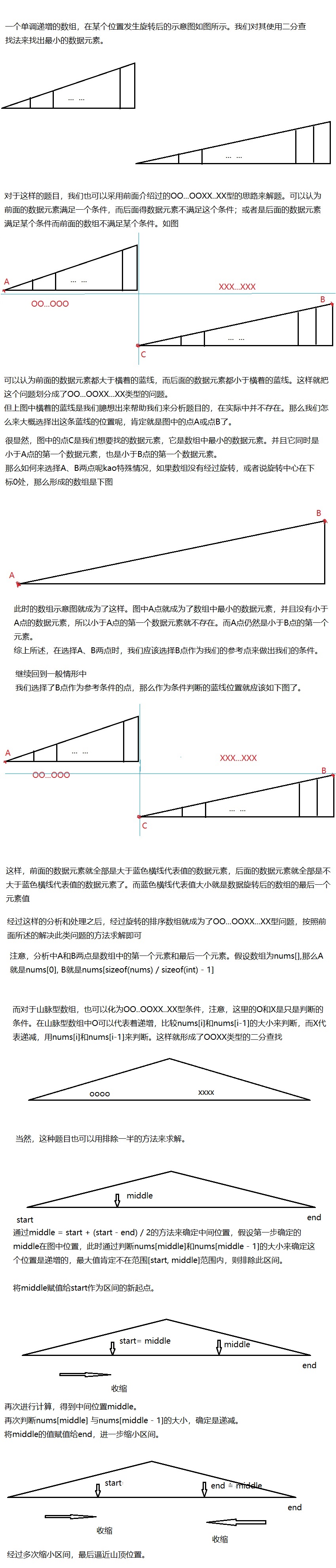
所谓旋转后的排序数组,首先这个数组是经过排序的,数组中所有的元素都是按照一定的顺序排列(递增或者递减),其次是这个数组经过了旋转,使得这个数组的排列性质出现了阶段性。如图:

对于这样的数组,要想找出数组中的最小值,可以直接采用暴力求解,使用for循环进行遍历,但是这样的算法的时间复杂度是O(n),并且如果采用这样的算法也没什么技术性可言。除了暴力求解,那么就是对这个旋转后的数组进行二分查找。其时间复杂度是O(logn),其思路如下图
还有一种类型是根据判断,保留有解的那一半而去掉无解的那一部分。