摘要
最近在学习 ng 的神经网络入门。先记录一笔,一些概念
CNN( conventional Neual Network) 卷积神经网络
RNN(Recurrent neural network) 递归神经网络
误差函数 logistic regression
为什么误差函数是平方和?
线性回归,误差函数是平方和函数,神经网络中也会选用平方和误差函数,但是为什么误差函数是平方和(即均方差),而不是绝对值、三次函数或者其他的形式呢?这个问题,有多个角度可以阐释。
1、从概率的角度
平方和不会出现正负抵消。另外,不管是线性回归,还是神经网络或者其他算法,我们可以假设实际的(理想的)模型是F(x)。在实际任务中,我们将从数据集{(Xi,Yi)},i = 1,2.......,n,中学习出一个模型f(x)。数据集可以认为是从理想的模型F(x)中采样,并添加高斯噪声而形成。
从这个角度看,数据集中的每一个点(Xi,Yi)均服从于均值为f(Xi),方差为某一固定值的高斯分布。所以数据(Xi, Yi)概率如下:
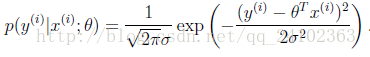
而判断一个模型是否足够接近理想模型,可以比较数据集在当前模型下出现的概率,也就是大家熟悉的极大似然估计了。所以,我们的目标就是极大化数据集的对数似然函数。此处就不继续展开,往下的推导就是一般的极大似然法。通过化简后,我们会发现,极大化数据集的对数似然函数,其实等价于最小化在数据集上,标签Yi与模型预测值f(Xi)差的平方和。
2、从技术实现的角度
在神经网络等部分算法中,经常会用梯度下降或者梯度上升来优化模型。在这个时候,平方和形式的误差函数就会在求导时体现出其快速、简洁的优势。不过这一点可以作为选择误差函数时的考量点之一,不是平方和误差函数的来源(数学背景)。
从平方和误差函数的数学背景可以看到,选用平方和误差函数,实际上是基于极大似然法。而极大似然法,天生自带过拟合的属性。所以这也是为什么在训练阶段,追求模型在训练集上的准确率时,模型容易过拟合的本质原因。而控制模型复杂度、调节参数等等操作,都是在过拟合与准确率之间做一个权衡。