求杨辉三角中数(n(1le nle1e9))最先出现的位置
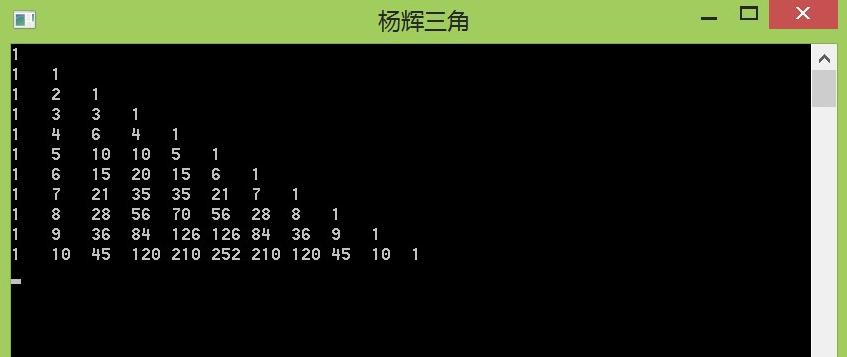
(dp[i][j]=dp[i][j-1]+dp[i-1][j-1]+....dp[1][j-1])
那么对于每一列单独考虑
第一列为(1;1;1;1...)
第二列为(1;2;3;4...)
第三列为(1;3;6;10...)
每一列的第(i)个元素都是上一列前(i)个元素的前缀和
除去一二列
那么第三列的元素到达(10^9)这个数量级差不多(1e5)个数 递增为(n^2)
第四列元素递增为(n^3)
第五列为(n^4)
那么利用前缀和,对于每一列求出值为(n)的位置(可能没有)
然后取最优解即可
复杂度为(n^{1/2}+n^{1/3}+n^{1/4}+n^{1/5}+n^{1/6}.....)
其实可以直接每一行每一列的for
(dp[i][j]=dp[i-1][j-1])
若是大于(n)直接break