一般问题模型:
在一张图上,有k次机会可以通过一条边而不需要计算权值或权值是一个特殊值,求从起点到终点的最短路。
变形问法:
在一张图上,有k次机会可以逆向行驶,求从起点到终点的最短路或最短路。
这种问题可以用两种方式解决。
第一种思想:动态规划(这里不详细解析,主要是介绍分层图)
第二种思想:分层图
先放一张图:(来自洛谷https://xiaohou.blog.luogu.org/fen-ceng-tu)
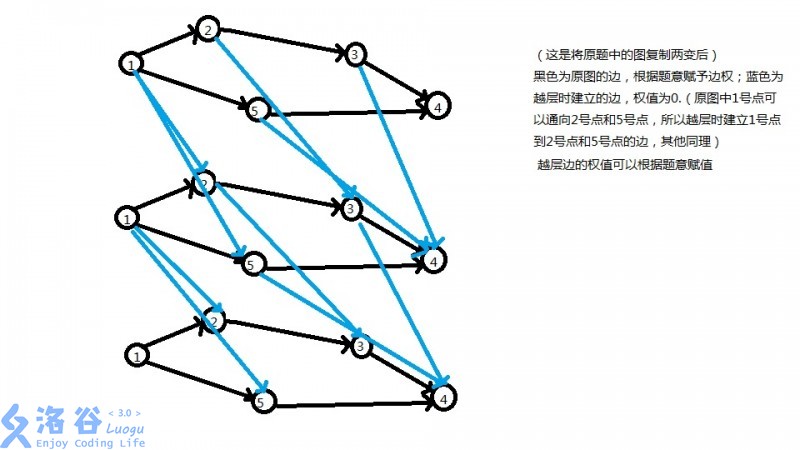
我们可以把这张原始图复制粘贴k次,每张图中权值与原始图相等
而图与图之间边权则要看题目的要求。
为了更深入理解,来看一道例题改造路Revamping Trails
一看题目,咦,k好小啊
把一个点强行拆分为k个,原图层代表使用0次升级路的机会,其他的图分别表示使用了1次、2次...k次升级路的机会,然后就可以连边了。考虑每层之间的关系,第i层与第i+1层的边的权值为0,等于用掉了一次升级路的机会。
然后因为这题卡SPFA,所以在跑一遍dijkstra就行了。
#include<bits/stdc++.h>
using namespace std;
const int MAXN=10000+10;
int n,m,k;
vector<int>ver[MAXN*21];
vector<int>edge[21*MAXN];
int d[MAXN*21];
bool vis[MAXN*21];
struct Node
{
int dis,pos;
bool operator <(const Node &x)const
{
return x.dis<dis;
}
};
inline int read()
{
int tot=0;
char c=getchar();
while(c<'0'||c>'9')
c=getchar();
while(c>='0'&&c<='9')
{
tot=(tot<<1)+(tot<<3)+c-'0';
c=getchar();
}
return tot;
}
inline void dijkstra()
{
priority_queue<Node>q;
q.push((Node){0,1});
while(q.size())
{
Node now=q.top();
q.pop();
int x=now.pos,y=now.dis;
if(vis[x])continue;
vis[x]=1;
for(int i=0;i<ver[x].size();i++)
{
int t=ver[x][i];
if(d[t]>y+edge[x][i])
{
d[t]=y+edge[x][i];
if(!vis[t])q.push((Node){d[t],t});
}
}
}
}
int main()
{
n=read();m=read();k=read();
memset(d,0x3f,sizeof(d));
d[1]=0;
for(int i=1;i<=m;i++)
{
int x=read(),y=read(),z=read();
ver[x].push_back(y);
edge[x].push_back(z);
ver[y].push_back(x);
edge[y].push_back(z);
for(int j=1;j<=k;j++)
{
ver[j*n+x].push_back(j*n+y);
edge[j*n+x].push_back(z);
ver[j*n+y].push_back(j*n+x);
edge[j*n+y].push_back(z);
ver[(j-1)*n+x].push_back(j*n+y);
edge[(j-1)*n+x].push_back(0);
ver[(j-1)*n+y].push_back(j*n+x);
edge[(j-1)*n+y].push_back(0);
}
}
/*for(int i=1;i<=2*n;i++)
{
for(int j=0;j<ver[i].size();j++)
{
cout<<i<<" "<<ver[i][j]<<" "<<edge[i][j]<<endl;
}
}*/
dijkstra();
int ans=d[n];
/*for(int i=1;i<=2*n;i++)cout<<d[i]<<" ";
cout<<endl;*/
for(int i=1;i<=k;i++)
{
ans=min(ans,d[i*n+n]);
}
cout<<ans<<endl;
return 0;
}