很好的一道数学推导题
45分做法
(O(N^4))
暴力枚举四个材料
55分做法
从第一个约束条件可得到所有可行答案都是单调递增的,所以可以排序一遍,减少枚举量,可以拿到55分
100分做法
首先可以发现每个x都小于n,而n最大值只是15000,所以可以开一个桶来存每个魔法值出现的次数
回忆一下3个约束条件
(xa<xb<xc<xd)①
(xb-xa=2(xd-xc))②
(xb-xa<(xc-xb)/3)③
现在魔改一下这三个式子
设(t=xd-xc)
所以②可化为(xb-xa=2t)④
将④代入③
(2t<(xc-xb)/3)
移项一下,就变成
(6t<xc-xb)⑤
再魔改一下
设(6t+k=xc-xb)(就是把差的部分补上去)
于是可以画出来一个图
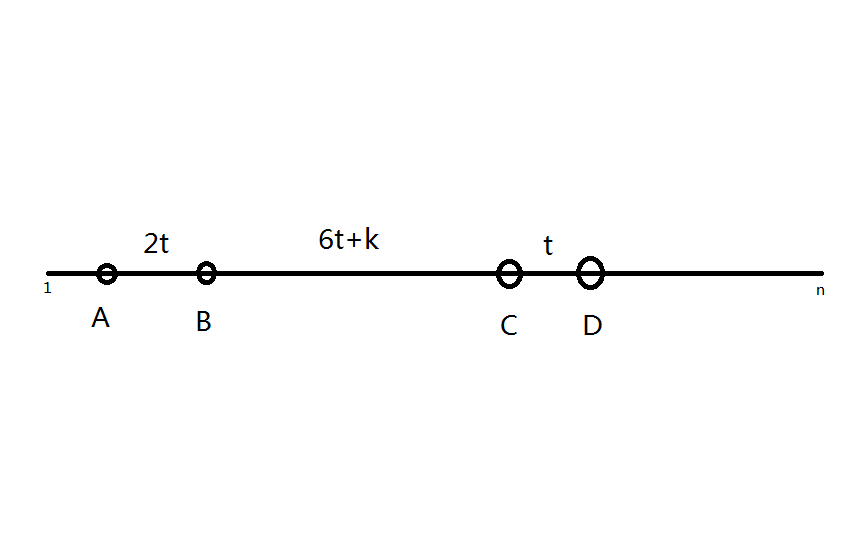
显然,A的最小值为1,D的最大值为n
由图可得(AD=9t+k)
所以我们可以尝试着枚举t,用t来表示各个魔法值的值
由上易得t的范围为(1<=t<=(n-1)/9)
再枚举D,因为我们已经枚举出了t,所以C的值是可以直接算出来的
(C=D-t)
又因为使A,B,C,D满足条件的k的最小值为1,所以对于当前的C和D,最大的A和B为(A=D-9t-1),(B=D-7t-1)
那么如果A和B更小怎么办?
观察到在其他条件不变的情况下,只要CC和BB满足(Xc-Xb>6t),那么这个魔法阵就一定成立,所以当((a1<a2,b1<b2))时,只要a2和b2能够和C,D组成魔法阵,a1,b1也一定能和C,D组成魔法阵,所以可以使用前缀和优化
然后又由乘法原理可得,当前魔法值作为DD物品的个数为(SumD=SumA*SumB*SumC)
所以我们利用前缀和优化(SumA*SumB)
C的情况可以顺便在算D的时候算出来
那么还有一个问题是,我们枚举的D的范围是多少?
因为要统计前缀和,所以一定是要顺推下去的,由上面那张图我们可以知道,D的最大值为n,最小值则为当k=1且A=1的时候,所以D的最小值为(9*t+2),再小是无法组成魔法阵的
同理可以枚举A
但是这个的情况又和枚举D的情况有一点不同
在其他条件不变的情况下,只要C和B满足(Xc−Xb>6t),那么这个魔法阵就一定成立,所以当((c1<c2,d1<d2))时,只要c1和d1能够和A,B组成魔法阵,c2,d2也一定能和A,B组成魔法阵,所以可以使用后缀和优化
因为需要统计后缀和,所以需要逆推
枚举的范围:A的最大值为((n−t∗9−1))(因为当k=1,D=n的时候A才最大),A的最小值则为1
所以就可以算出每个魔法值作为A,B,C,D物品的次数了,输出时直接输出当前魔法物品的魔法值的次数就可以了
代码:
#include<bits/stdc++.h>
using namespace std;
const int MAXN=15000+10;
const int MAXM=40000+10;
int n,m;
int x[MAXM],v[MAXN];
int a[MAXN],b[MAXN],c[MAXN],d[MAXN];
inline int read()
{
int tot=0;
char c=getchar();
while(c<'0'||c>'9')
c=getchar();
while(c>='0'&&c<='9')
{
tot=tot*10+c-'0';
c=getchar();
}
return tot;
}
int main()
{
n=read();m=read();
for(int i=1;i<=m;i++)
{
x[i]=read();
v[x[i]]++;
}
for(int t=1;t<=(n-1)/9;t++)
{
int sum=0;
for(int D=9*t+2;D<=n;D++)
{
int A=D-9*t-1,B=D-7*t-1,C=D-t;
sum+=v[A]*v[B];
c[C]+=v[D]*sum;
d[D]+=v[C]*sum;
}
sum=0;
for(int A=n-9*t-1;A>=1;A--)
{
int B=A+2*t,C=8*t+1+A,D=9*t+1+A;
sum+=v[C]*v[D];
a[A]+=v[B]*sum;
b[B]+=v[A]*sum;
}
}
for(int i=1;i<=m;i++)
cout<<a[x[i]]<<" "<<b[x[i]]<<" "<<c[x[i]]<<" "<<d[x[i]]<<endl;
return 0;
}